题目内容
设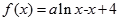 ,(
,(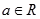 ),曲线
),曲线 在点
在点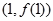 处的切线垂直于
处的切线垂直于 轴.
轴.
(Ⅰ) 求 的值;
的值;
(Ⅱ) 求函数 的极值。
的极值。
(Ⅰ) (Ⅱ)极大值3
(Ⅱ)极大值3
解析试题分析:
解:(Ⅰ)
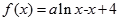 ,
,
 ………………………………………………………………2分
………………………………………………………………2分
由于曲线 在点
在点 处的切线垂直于
处的切线垂直于 轴,故该切线斜率为0,即
轴,故该切线斜率为0,即 ,…………………………………………………………………………5分
,…………………………………………………………………………5分
 …………………………………………………………………………………6分
…………………………………………………………………………………6分
(Ⅱ)由(Ⅰ)知, ,
,
令 故
故 在
在 上为增函数;…………………………9分
上为增函数;…………………………9分
令 ,故
,故 在
在 上为减函数;…………………………12分
上为减函数;…………………………12分
故 在
在 处取得极大值
处取得极大值 。…………………………………………13分
。…………………………………………13分
考点:利用函数导数求切线斜率,判定单调性,求极值最值
点评:要求学生掌握常见函数的求导公式及导数与单调性的关系

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
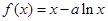 ,
,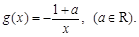
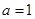 ,求函数
,求函数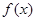 的极值;
的极值; ,求函数
,求函数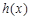 的单调区间;
的单调区间;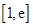 (
( )上存在一点
)上存在一点 ,使得
,使得
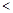
 成立,求
成立,求 的取值范围.
的取值范围.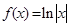
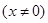 ,函数
,函数
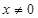 时,求函数
时,求函数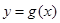 的表达式;
的表达式;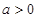 ,且函数
,且函数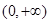 上的最小值是2 ,求
上的最小值是2 ,求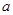 的值;
的值;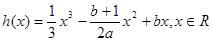 ,恰有三个零点,求b的取值范围。
,恰有三个零点,求b的取值范围。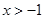 ,证明:
,证明: 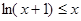
 是实数,函数
是实数,函数 。
。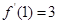 ,求
,求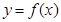 在点
在点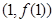 处的切线方程;
处的切线方程; 在区间
在区间 上的最大值。
上的最大值。 的图象过点
的图象过点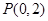 ,且在点
,且在点 处的切线方程为
处的切线方程为 .
.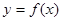 的解析式;(Ⅱ)求函数
的解析式;(Ⅱ)求函数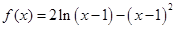 .
.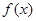 的单调递增区间;
的单调递增区间;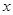 的方程
的方程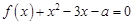 在区间
在区间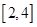 内恰有两个相异的实根,求实数
内恰有两个相异的实根,求实数 的取值范围.
的取值范围. (单位:m/s)紧急刹车至停止。求:
(单位:m/s)紧急刹车至停止。求: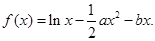
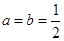 时,求函数
时,求函数 的最大值;
的最大值;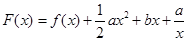 ,(
,(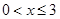 )其图象上任意一点
)其图象上任意一点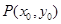 处切线的斜率
处切线的斜率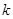 ≤
≤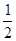 恒成立,求实数
恒成立,求实数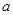 的取值范围;
的取值范围;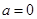 ,
,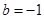 ,方程
,方程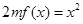 有唯一实数解,求正数
有唯一实数解,求正数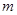 的值.
的值.