Question

【题目】已知椭圆O： （a＞b＞0）过点（ ，﹣ ），A（x0 ， y0）（x0y0≠0），其上顶点到直线 x+y+3=0的距离为2，过点A的直线l与x，y轴的交点分别为M、N，且 =2 ．
（1）证明：|MN|为定值；
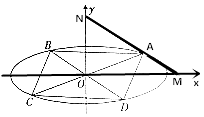
（2）如图所示，若A，C关于原点对称，B，D关于原点对称，且 =λ ，求四边形ABCD面积的最大值．

Answer 1

【答案】
（1）证明：其上顶点（0，b）到直线 x+y+3=0的距离为2，∴ ，解得b=1．

又椭圆O： （a＞b＞0）过点（ ，﹣ ），∴ =1，解得a2=4．

∴椭圆的标准方程为： =1．

点A在椭圆上，∴ =1．

设经过点A的直线方程为：y﹣y0=k（x﹣x0），

可得M ，N（0，y0﹣kx0）．

∵ =2 ，∴﹣x0= ，即k=﹣ ．

∴|MN|= = =3为定值

（2）解：设∠AOD=α．∵ =λ ，∴2|OD|=3λ．

由题意可得：S四边形ABCD= =2× |OA|sinα≤3λ|OA|

【解析】（1）其上顶点（0，b）到直线 x+y+3=0的距离为2，利用点到直线的距离公式可得 ，根据椭圆O： （a＞b＞0）过点（ ，﹣ ），解得a2 ． 可得椭圆的标准方程为： =1．设经过点A的直线方程为：y﹣y0=k（x﹣x0），可得M ，N（0，y0﹣kx0）．利用 =2 ，可得k=﹣ ．利用两点之间的距离公式可得|MN|．（2）设∠AOD=α．由 =λ ，可得2|OD|=3λ．由题意可得：S四边形ABCD= =2× |OA|sinα，即可得出．