题目内容

已知函数f（x）=x3+ax2-2ax+3a2，且在f（x）图象一点（1，f（1））处的切线在y轴上的截距小于0，则a的取值范围是


  1. A.
    （-1，1）
  2. B.
    数学公式
  3. C.
    数学公式
  4. D.
    数学公式
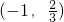
C
分析：先求函数的导函数f′（x），再求所求切线的斜率即f′（1），由于切点为（1，f（1）），故由点斜式即可得所求切线的方程，最后利用切线在y轴上的截距小于0建立不等关系求解即可．
解答：由题意f'（x）=3x2+2ax-2a
∴f′（1）=3，f（1）=3a2-a+1，
即函数f（x）图象在点（1，f（1））处的切线斜率为3，
∴图象在点（1，f（1））处的切线方程为y-（3a2-a+1）=3（x-1），
令x=0得y=3a2-a-2，
由题意得3a2-a-2＜0，解得：a∈，
故选C．
点评：此题考查学生会利用导数求曲线上过某点切线方程的斜率，考查计算能力和等价转化能力，是一道中档题．
练习册系列答案
相关题目
精英家教网已知函数f（x）=Asin（ωx+φ）（x∈R，A＞0，ω＞0，|φ|＜
π
2
）的部分图象如图所示，则f（x）的解析式是（　　）
A、f(x)=2sin(πx+
π
6
)(x∈R)
B、f(x)=2sin(2πx+
π
6
)(x∈R)
C、f(x)=2sin(πx+
π
3
)(x∈R)
D、f(x)=2sin(2πx+
π
3
)(x∈R)
（2012•深圳一模）已知函数f(x)=
1
3
x3+bx2+cx+d，设曲线y=f（x）在与x轴交点处的切线为y=4x-12，f′（x）为f（x）的导函数，且满足f′（2-x）=f′（x）．
（1）求f（x）；
（2）设g(x)=x
f′(x)
 ， m＞0，求函数g（x）在[0，m]上的最大值；
（3）设h（x）=lnf′（x），若对一切x∈[0，1]，不等式h（x+1-t）＜h（2x+2）恒成立，求实数t的取值范围．
（2011•上海模拟）已知函数f(x)=(
x
a
-1)2+(
b
x
-1)2，x∈(0，+∞)，其中0＜a＜b．
（1）当a=1，b=2时，求f（x）的最小值；
（2）若f（a）≥2m-1对任意0＜a＜b恒成立，求实数m的取值范围；
（3）设k、c＞0，当a=k2，b=（k+c）2时，记f（x）=f1（x）；当a=（k+c）2，b=（k+2c）2时，记f（x）=f2（x）．
求证：f1(x)+f2(x)＞
4c2
k(k+c)
．
已知函数f(x)=(
x
a
-1)2+(
b
x
-1)2，x∈(0，+∞)，其中0＜a＜b．
（1）当a=1，b=2时，求f（x）的最小值；
（2）若f（a）≥2m-1对任意0＜a＜b恒成立，求实数m的取值范围；
（3）设k、c＞0，当a=k2，b=（k+c）2时，记f（x）=f1（x）；当a=（k+c）2，b=（k+2c）2时，记f（x）=f2（x）．
求证：f1(x)+f2(x)＞
4c2
k(k+c)
．
已知函数f(x)=
1
3
x3+bx2+cx+d，设曲线y=f（x）在与x轴交点处的切线为y=4x-12，f′（x）为f（x）的导函数，且满足f′（2-x）=f′（x）．
（1）求f（x）；
（2）设g(x)=x
f′(x)
 ， m＞0，求函数g（x）在[0，m]上的最大值；
（3）设h（x）=lnf′（x），若对一切x∈[0，1]，不等式h（x+1-t）＜h（2x+2）恒成立，求实数t的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网