题目内容

△ABC中，三边长分别为AB=
7
，BC=
3
 CA=
2
，则
AB
•
BC
+
2
BC
•
CA
+
3
CA
•
AB
的值为
 
．
考点：平面向量数量积的运算
专题：计算题,平面向量及应用
分析：根据题意，画出图形，结合图形，求出三角形的内角的余弦值，即可求出计算结果．
解答： 解：△ABC中，三边长分别为AB=
7
，BC=
3
 CA=
2
，
∴cosα=
(
7
)2+(
2
)2-(
3
)2
2×
7
×
2
=
3
14

cosβ=
(
7
)2+(
3
)2-(
2
)2
2×
7
×
3
=
4
21

cosγ=
(
3
)2+(
2
)2-(
7
)2
2×
3
×
2
=-
1
6

∴
AB
•
BC
+
2
BC
•
CA
+
3
CA
•
AB
=
7
×
3
cos（π-β）+
2
×
3
×
2
cos（π-γ）+
3
×
2
×
7
cos（π-α）
=
7
×
3
×（-
4
21
）+
2
×
3
×
2
×
1
6
+
3
×
2
×
7
×（-
3
14
）
=-4+
2
-3
3
．
故答案为：-4+
2
-3
3
．
点评：本题考查了平面向量的应用问题，解题时应根据图形，结合向量的数量积的运算法则，进行计算即可，是基础题．
练习册系列答案
相关题目
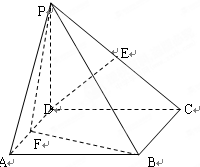如图，四棱锥P-ABCD中，四边形ABCD为正方形，PD⊥面ABCD，PD=DA=2，F，E分别为AD，PC的中点．
（1）证明：DE∥面PFB．          
（2）求点E到平面PFB的距离．
已知函数f（x）=xlnx，当x2＞x1＞0时，给出以下几个结论：
①（x1-x2）•[f（x1）-f（x2）]＜0
②
f(x1)-f(x2)
x1-x2
＜1
③f（x1）+x2＜f（x2）+x1；
④x2f（x1）＜x1f（x2）；
⑤当lnx1＞-1时，x1f（x1）+x2f（x2）＞2x2f（x1）
其中正确的是
 
．
等差数列{an}中，a2=1，a5=4，则该等差数列{an}的公差为
 
．
设
.
a
=（1，5，-1），
b
=（-2，3，5），若（k
a
+
b
）∥（
a
-3
b
），则k=
 
．
已知双曲线C：
x2
a2
-
y2
b2
=1（a＞0，b＞0）的左焦点为F，C与过原点的直线相交于A、B两点，连结AF、BF，若|AB|=10，|AF|=6，cos∠ABF=
4
5
，则C的离心率e=
 
．
等比数列1，3，9…的第4项到第7项的和为
 
．
若a=log
1
2
3，b=1.3
2
3
，c=(
2
3
)1.3，则a，b，c用“＞“号连接的正确表达式为
 
．
已知函数f（x）=
1
4x+2
，若函数y=f（x+m）-
1
4
为奇函数，则实数m为（　　）
A、-
1
2
B、0
C、
1
2
D、1

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网