题目内容

已知函数，a∈（2，+∞）；，b∈R

 （1）试比较与大小；

（2）若.

解： 设a1、a2∈（2，+∞）且a1＜a2.

∴；

∴

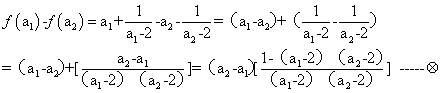
∵2＜a1＜a2.∴a2-a1 ＞0  ∴ ＞0

当a1、a2∈（2，3）时     0＜ ＜1∴＞0

∴＞0  ∴∴ 在（2，3）单调递减

当a1、a2∈（3，+∞）时     1＜ ∴＜0

∴＜0  ∴∴ 在（3，+∞）单调递增

∴当x=3时，有最小值

又  ∴

∵

∴＞

（2）

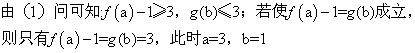
练习册系列答案
相关题目

已知函数

(Ⅰ)若a＝2，求f(x)的定义域；

(Ⅱ)若f(x)在区间(0，1]上是减函数，求实数a的取值范围．

已知函数则“a≤－2”是“f(x)在R上单调递减”的

[　　]

A．充分而不必要条件

B．必要而不充分条件

C．充分必要条件

D．既不充分也不必要条件

已知函数

(Ⅰ)当a＝2时，求函数的最大值和最小值；

(Ⅱ)若函数g(x)＝af(x)，求函数g(x)的单调递减区间；

(Ⅲ)当a＝1时，求证：

已知函数

(1).a≥－2时,求F(x)= f(x)- g(x)的单调区间;

(2).设h(x)= f(x)+ g(x),且h(x)有两个极值点为x1 , x2 ,其中,求h(x1)- h(x2)的最小值.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网