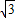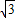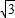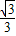题目内容
若P是椭圆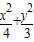
=1上的点，F1和F2是焦点，则k=|PF1|•|PF2|的最大值和最小值分别是 和 ．
【答案】分析：由题意，设|PF1|=x，故有|PF1|•|PF2|=x（4-x）=-x2+4x=-（x-2）2+4，确定x的范围，即可求得k的最值．
解答：解：由题意，设|PF1|=x，
∵|PF1|+|PF2|=2a=4，∴|PF2|=4-x
∴|PF1|•|PF2|=x（4-x）=-x2+4x=-（x-2）2+4
∵a=2，b=
，∴c=
=1
∴1≤x≤3
∴x=1或3时，k=-x2+4x取最小值3；x=2时，k=-x2+4x取最大值为4
故答案为：4，3．
点评：本题以椭圆的标准方程为载体，考查椭圆定义的运用，考查函数的构建，考查函数的单调性，属于基础题．
解答：解：由题意，设|PF1|=x，
∵|PF1|+|PF2|=2a=4，∴|PF2|=4-x
∴|PF1|•|PF2|=x（4-x）=-x2+4x=-（x-2）2+4
∵a=2，b=
，∴c==1∴1≤x≤3
∴x=1或3时，k=-x2+4x取最小值3；x=2时，k=-x2+4x取最大值为4
故答案为：4，3．
点评：本题以椭圆的标准方程为载体，考查椭圆定义的运用，考查函数的构建，考查函数的单调性，属于基础题．
练习册系列答案
学而优暑期衔接南京大学出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
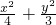=1上的点，F1和F2是焦点，则k=|PF1|•|PF2|的最大值和最小值分别是________和________．
+
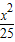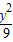=1上的点，F1、F2分别是椭圆的左、右焦点，若
=
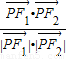，则△F1PF2的面积为（ ）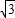
+
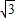
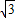
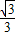
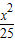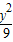=1上的点，F1、F2分别是椭圆的左、右焦点，若
=
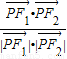，则△F1PF2的面积为（ ）
=1上的点.若F1、F2是椭圆的两个焦点,则|PF1|+|PF2|等于( )