题目内容
12.某三棱锥的三视图如图所示,则该三棱锥的表面积为3+$\sqrt{2}+\sqrt{3}$.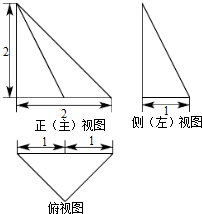
分析 由已知中的三视图,可知该几何体是一个以俯视图为底面的三棱锥,求出各个面的面积,相加可得答案.
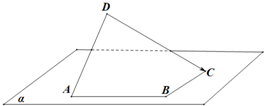
解答 解:由已知中的三视图,可知该几何体的直面图如下所示:
由主视图知CD⊥平面ABC,设AC中点为E,则BE⊥AC,且AE=CE=1;
由主视图知CD=2,由左视图知BE=1,
在Rt△BCE中,BC=$\sqrt{2}$,
在Rt△BCD中,BD=$\sqrt{6}$,
在Rt△ACD中,AD=2$\sqrt{2}$.
故棱锥的四个面均为直角三角形,
故三棱锥的表面积S=$\frac{1}{2}$(2×1+2×2+2×$\sqrt{2}$+$\sqrt{2}$×$\sqrt{6}$)=3+$\sqrt{2}+\sqrt{3}$,
故答案为:3+$\sqrt{2}+\sqrt{3}$
点评 本题考查的知识点是由三视图求体积和表面积,解决本题的关键是得到该几何体的形状.

练习册系列答案
相关题目
20.已知条件p:|x+1|≤2,条件q:x≤a,且p是q的充分不必要条件,则a的取值范围是( )
| A. | a≥1 | B. | a≤1 | C. | a≥-1 | D. | a≤-3 |
2.已知函数f(x)=x3+bx2+cx,对任意的b,c∈[-3,3].f(x)在(-1,1)内既有极大值又有极小值的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{6}$ |
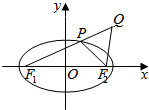 已知椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1(a>b>0)的左、右焦点分别是F1,F2,Q是椭圆外的动点,满足|$\overrightarrow{{F}_{1}Q}$|=10.点P是线段F1Q与该椭圆的交点,点T在线段F2Q上,并且满足$\overrightarrow{PT}$•$\overrightarrow{T{F}_{2}}$=0,|$\overrightarrow{T{F}_{2}}$|=0.
已知椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1(a>b>0)的左、右焦点分别是F1,F2,Q是椭圆外的动点,满足|$\overrightarrow{{F}_{1}Q}$|=10.点P是线段F1Q与该椭圆的交点,点T在线段F2Q上,并且满足$\overrightarrow{PT}$•$\overrightarrow{T{F}_{2}}$=0,|$\overrightarrow{T{F}_{2}}$|=0.