题目内容
求下列函数的最值:(1)求函数y=ax(b-cx)的最大值;(ac>0,cx>0,b-cx>0)
(2)若x、y∈R +且x2+![]() =1,求x
=1,求x![]() 的最大值.
的最大值.
解:(1)由已知y=![]() ·cx(b-cx)≤
·cx(b-cx)≤![]() ·[
·[![]() ]2=
]2=![]() ,当且仅当cx=b-cx,即x=
,当且仅当cx=b-cx,即x=![]() 时,等号成立.∴ymax=
时,等号成立.∴ymax=![]() (注:利用二次函数求最值的方法也可).
(注:利用二次函数求最值的方法也可).
(2)方法一:y2=2-2x2,∴x![]() =x
=x![]() =
=![]()
![]() )≤
)≤![]() ·
·![]() =
=![]()
![]() .
.
当且仅当2x2=3-2x2,即x=![]() ,y=
,y=![]() 时,等号成立.
时,等号成立.
∴x![]() 的最大值为
的最大值为![]()
![]() .
.
方法二:x![]() =
=![]() (
(![]() x)
x)![]() ≤
≤![]() ·
·![]() =
=![]() ·
·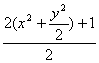
=![]()
![]() .
.
当且仅当![]() x=
x=![]() ,即x=
,即x=![]() ,y=
,y=![]() 时,等号成立.∴x
时,等号成立.∴x![]() 的最大值为
的最大值为![]()
![]() .
.

练习册系列答案
相关题目