题目内容
设圆Q过点P(0,2),且在x轴上截得的弦RG的长为4.(1)求圆心Q的轨迹E的方程;
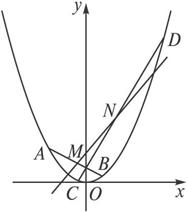
(2)过点F(0,1),作轨迹E的两条互相垂直的弦AB、CD,设AB、CD的中点分别为M、N,试判断直线MN是否过定点?并说明理由.
解:(1)设圆心Q的坐标为(x,y),如图,过圆心Q作QH⊥x轴于H,
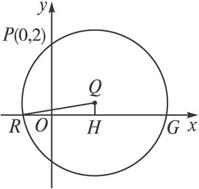
则H为RG的中点,在Rt△RHQ中,QR2=QH2+RH2.2分∵QR=QP,RH=2,
∴x2+(y-2)2=y2+4,即x2=4y.
(2)设A(xA,yA),B(xB,yB),M(xM,yM),N(xN,yN),直线AB的方程为y=kx+1(k≠0),则xA2=4yA,①
xB2=4yB.②
由①-②得xA+xB=![]() =4k,∴xm=2k.∵点M(xM,yM)在直线y=kx+1上,
=4k,∴xm=2k.∵点M(xM,yM)在直线y=kx+1上,
∴yM=kxM+1=2k2+1.∴点M的坐标为(2k,2k2+1).
同理可得xC+xD=![]() ,xn=
,xn=![]() ,yn=
,yn=![]() xN+1=
xN+1=![]() +1.
+1.
∴点N的坐标为(![]() ,
,![]() +1).
+1).
直线MN的斜率为kMN=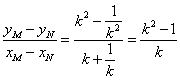 ,其方程为
,其方程为
y-2k2-1=![]() (x-2k),整理得k(y-3)=(k2-1)x,显然,不论k为何值,点(0,3)均满足方程,
(x-2k),整理得k(y-3)=(k2-1)x,显然,不论k为何值,点(0,3)均满足方程,
∴直线MN恒过定点(0,3).

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
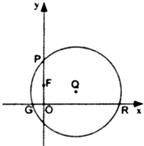 设圆Q过点P(0,2),且在x轴上截得的弦RG的长为4.
设圆Q过点P(0,2),且在x轴上截得的弦RG的长为4.