题目内容
已知关于坐标轴对称的椭圆经过两点A(0,2)和B(| 1 |
| 2 |
| 3 |
(1)求椭圆的标准方程
(2)若点P是椭圆上的一点,F1和F2是焦点,且∠F1PF2=30°,求△F1PF2的面积、
分析:(1)设经过A(0,2),B(
,
)的椭圆标准方程为mx2+ny2=1,代入A、B得
,由此能求出椭圆方程.
(2)在椭圆x2+
=1中,a=2,b=1,c=
=
,由点P在椭圆上,知|PF1|+|PF2|=2a=4.由余弦定理知:|PF1|2+|PF2|2-2|PF1||PF2|cos30°=|F1F2|2=(2c)2=1,由此得(2+
)|PF1|•|PF2|=4,从而得到S△PF1F2=
|PF1|•|PF2|sin30°=2-
.
| 1 |
| 2 |
| 3 |
|
(2)在椭圆x2+
| y2 |
| 4 |
| a2-b2 |
| 3 |
| 3 |
| 1 |
| 2 |
| 3 |
解答:解:(1)设经过两点A(0,2),B(
,
)的椭圆标准方程为
mx2+ny2=1,代入A、B得
?
,
∴所求椭圆方程为x2+
=1、(5分)
(2)在椭圆x2+
=1中,a=2,b=1、∴c=
=
又∵点P在椭圆上,∴|PF1|+|PF2|=2a=4、①(6分)
由余弦定理知:|PF1|2+|PF2|2-2|PF1||PF2|cos30°=|F1F2|2=(2c)2=12 ②(8分)
把①两边平方得|PF1|2+|PF2|2+2|PF1|•|PF2|=16,③
③-②得(2+
)|PF1|•|PF2|=4,
∴|PF1|•|PF2|=4(2-
),(10分)
∴S△PF1F2=
|PF1|•|PF2|sin30°=2-
、(12分)
| 1 |
| 2 |
| 3 |
mx2+ny2=1,代入A、B得
|
|
∴所求椭圆方程为x2+
| y2 |
| 4 |
(2)在椭圆x2+
| y2 |
| 4 |
| a2-b2 |
| 3 |
又∵点P在椭圆上,∴|PF1|+|PF2|=2a=4、①(6分)
由余弦定理知:|PF1|2+|PF2|2-2|PF1||PF2|cos30°=|F1F2|2=(2c)2=12 ②(8分)
把①两边平方得|PF1|2+|PF2|2+2|PF1|•|PF2|=16,③
③-②得(2+
| 3 |
∴|PF1|•|PF2|=4(2-
| 3 |
∴S△PF1F2=
| 1 |
| 2 |
| 3 |
点评:本题考查椭圆和直线的位置关系,解题时要认真审题,仔细求解,注意公式的灵活选用.

练习册系列答案
相关题目
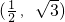 ;
; ;
;