题目内容
 在如图所示的几何体中,四边形ABCD是菱形,ADNM是矩形,平面ADNM⊥平面ABCD,∠DAB=60°,AD=2,AM=1,E为AB的中点.
在如图所示的几何体中,四边形ABCD是菱形,ADNM是矩形,平面ADNM⊥平面ABCD,∠DAB=60°,AD=2,AM=1,E为AB的中点.
(Ⅰ)求证:AN∥平面MEC;
(Ⅱ)在线段AM上是否存在点P,使二面角P-EC-D的大小为 ?若存在,求出AP的长h;若不存在,请说明理由.
?若存在,求出AP的长h;若不存在,请说明理由.
 解:(I)CM与BN交于F,连接EF.
解:(I)CM与BN交于F,连接EF.由已知可得四边形BCNM是平行四边形,
所以F是BN的中点.
因为E是AB的中点,
所以AN∥EF.…(7分)
又EF?平面MEC,AN?平面MEC,
所以AN∥平面MEC.…(9分)
 (II)由于四边形ABCD是菱形,E是AB的中点,可得DE⊥AB.
(II)由于四边形ABCD是菱形,E是AB的中点,可得DE⊥AB.又四边形ADNM是矩形,面ADNM⊥面ABCD,∴DN⊥面ABCD,
如图建立空间直角坐标系D-xyz,则D(0,0,0),E(
 ,0,0),C(0,2,0),P(
,0,0),C(0,2,0),P( ,-1,h),
,-1,h),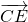 =(
=( ,-2,0),
,-2,0),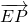 =(0,-1,h),设平面PEC的法向量为
=(0,-1,h),设平面PEC的法向量为 =(x,y,z).
=(x,y,z).则
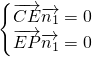 ,∴
,∴ ,
,令y=
 h,∴
h,∴ =(2h,
=(2h, h,
h, ),又平面ADE的法向量
),又平面ADE的法向量 =(0,0,1),
=(0,0,1),∴cos<
 ,
, >=
>=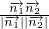 =
= <1,
<1,∴在线段AM上是否存在点P,使二面角P-EC-D的大小为
 .
.分析:(I)利用CM与BN交于F,连接EF.证明AN∥EF,通过直线与平面平行的判定定理证明AN∥平面MEC;
(II)对于存在性问题,可先假设存在,即假设x在线段AM上是否存在点P,使二面角P-EC-D的大小为
 .再通过建立空间直角坐标系,求出相关点的坐标,结合向量的数量积求出二面角P-EC-D的大小,若出现矛盾,则说明假设不成立,即不存在;否则存在.
.再通过建立空间直角坐标系,求出相关点的坐标,结合向量的数量积求出二面角P-EC-D的大小,若出现矛盾,则说明假设不成立,即不存在;否则存在.点评:本题考查存在性问题,直线与平面平行的判断,二面角的求法,考查空间想象能力与计算能力.

练习册系列答案
相关题目
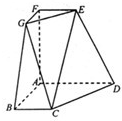 在如图所示的几何体中,四边形ABCD、ADEF、ABGF均为全等的直角梯形,且BC∥AD,AB=AD=2BC.
在如图所示的几何体中,四边形ABCD、ADEF、ABGF均为全等的直角梯形,且BC∥AD,AB=AD=2BC.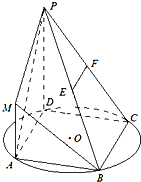 在如图所示的几何体中,平行四边形ABCD的顶点都在以AC为直径的圆O上,AD=CD=DP=a,AP=CP=
在如图所示的几何体中,平行四边形ABCD的顶点都在以AC为直径的圆O上,AD=CD=DP=a,AP=CP= (2012•朝阳区一模)在如图所示的几何体中,四边形ABCD为平行四边形,∠ABD=90°,EB⊥平面ABCD,EF∥AB,AB=2,EF=1,
(2012•朝阳区一模)在如图所示的几何体中,四边形ABCD为平行四边形,∠ABD=90°,EB⊥平面ABCD,EF∥AB,AB=2,EF=1, 在如图所示的几何体中,面CDEF为正方形,面ABCD为等腰梯形,AB∥CD,AB=2BC,∠ABC=60°,AC⊥FB.
在如图所示的几何体中,面CDEF为正方形,面ABCD为等腰梯形,AB∥CD,AB=2BC,∠ABC=60°,AC⊥FB.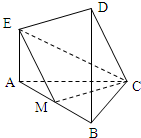 在如图所示的几何体中,EA⊥平面ABC,DB⊥平面ABC,AC⊥BC,AC=BC=BD=2AE=2,M是AB的中点.
在如图所示的几何体中,EA⊥平面ABC,DB⊥平面ABC,AC⊥BC,AC=BC=BD=2AE=2,M是AB的中点.