题目内容
已知椭圆的长轴长为2a,焦点是F1(-(1)求椭圆的方程;
(2)求直线l的方程.
解:(1)∵F1到直线x=-![]() 的距离为
的距离为![]() ,?
,?
∴-![]() +
+![]() =
=![]() ,∴a2=4.?
,∴a2=4.?
而c=![]() ,
,
∴b2=a2-c2=1.
∵椭圆的焦点在x轴上,?
∴所求椭圆的方程为![]() +y2=1.
+y2=1.
(2)设A(x1,y1),B(x2,y2).
l的方程为y=k(x-![]() )(k>0).
)(k>0).
由|F2B|=3|F2A|得y2=-3y1,
即k(x2-![]() )=-3k(x1-
)=-3k(x1-![]() ).
).
∴3x1+x2=4![]() . ①?
. ①?
由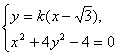
得(4k2+1)x2-8![]() k2x+4(3k2-1)=0.?
k2x+4(3k2-1)=0.?
∴x1+x2=![]() ②
②
x1x2=![]() ③
③
由①②③解得k2=2,?
∴k=![]() .?
.?
∴直线l的方程为y=![]() (x-
(x-![]() ).
).

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
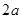 ,焦点是
,焦点是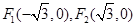 ,点
,点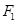 到直线
到直线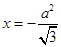 的距离为
的距离为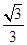 ,过点
,过点 且倾斜角为锐角的直线
且倾斜角为锐角的直线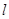 与椭圆交于
与椭圆交于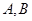 两点,使得
两点,使得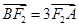 .
.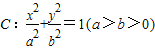 的长轴长为4.
的长轴长为4.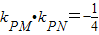 时,求椭圆的方程.
时,求椭圆的方程.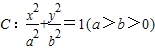 的长轴长为4.
的长轴长为4.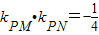 时,求椭圆的方程.
时,求椭圆的方程. 的长轴长为4.
的长轴长为4.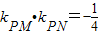 时,求椭圆的方程.
时,求椭圆的方程.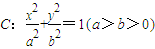 的长轴长为4.
的长轴长为4.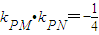 时,求椭圆的方程.
时,求椭圆的方程.