题目内容
(本小题满分14分)
无穷数列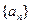 的前n项和
的前n项和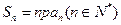 ,并且
,并且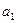 ≠
≠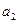 .
.
(1)求p的值;
(2)求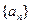 的通项公式;
的通项公式;
(3)作函数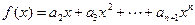 ,如果
,如果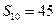 ,证明:
,证明: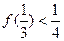 .
.
无穷数列
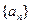 的前n项和
的前n项和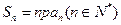 ,并且
,并且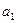 ≠
≠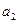 .
.(1)求p的值;
(2)求
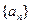 的通项公式;
的通项公式;(3)作函数
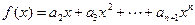 ,如果
,如果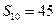 ,证明:
,证明: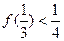 .
.解:(1)∵ 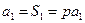 ∴
∴ 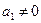 ,且p=1,或
,且p=1,或 .
.
若是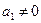 ,且p=1,则由
,且p=1,则由 .
.
∴ ,矛盾.故不可能是:
,矛盾.故不可能是: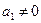 ,且p=1.由
,且p=1.由 ,得
,得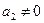 .
.
又 ,∴
,∴  .
.
(2)∵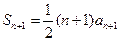 ,
,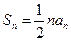 ,
,
∴ .
.
 .
.
当k≥2时,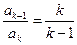 . ∴ n≥3时有
. ∴ n≥3时有
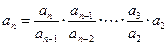
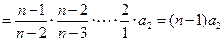 .
.
∴ 对一切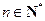 有:
有: .
.
(3)∵ ,
,
∴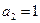 .
.  .
.
故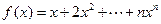 .
.
∴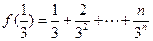 . 故
. 故 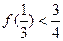 .
.
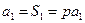 ∴
∴ 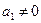 ,且p=1,或
,且p=1,或 .
.若是
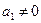 ,且p=1,则由
,且p=1,则由 .
.∴
 ,矛盾.故不可能是:
,矛盾.故不可能是: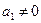 ,且p=1.由
,且p=1.由 ,得
,得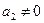 .
.又
 ,∴
,∴  .
.(2)∵
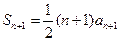 ,
,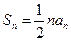 ,
,∴
 .
. .
.当k≥2时,
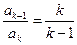 . ∴ n≥3时有
. ∴ n≥3时有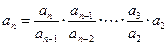
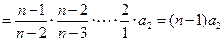 .
.∴ 对一切
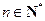 有:
有: .
.(3)∵
 ,
,∴
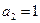 .
.  .
.故
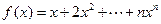 .
.∴
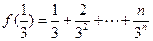 . 故
. 故 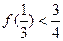 .
.略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
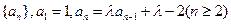 .
.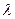 为何值时,数列
为何值时,数列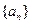 可以构成公差不为零的等差数列,并求其通项公式;
可以构成公差不为零的等差数列,并求其通项公式;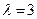 ,令
,令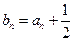 ,求数列
,求数列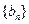 的前
的前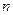 项和
项和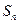 .
.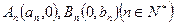 ,其中数列
,其中数列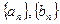 都是递增数列。
都是递增数列。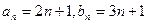 ,判断直线
,判断直线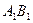 与
与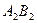 是否平行;
是否平行;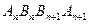 的面积为
的面积为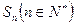 .
.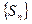 也是等差数列;
也是等差数列;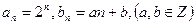 ,
,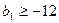 ,记直线
,记直线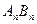 的斜率为
的斜率为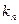 ,数列
,数列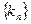 前8项依次递减,求满足条件的数列
前8项依次递减,求满足条件的数列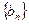 的个数。
的个数。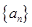 的前
的前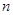 项和为
项和为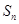 ,若
,若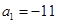 ,
,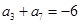 ,则当
,则当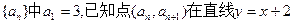 上,
上,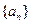 的通项公式;
的通项公式;
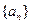 为等比数列,
为等比数列,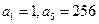 ;
;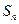 为等差数列
为等差数列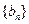 的前n项和,
的前n项和,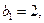
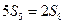 .
.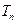
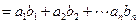 ,求
,求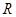 上的函数
上的函数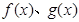 满足
满足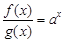 ,且
,且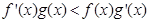 ,
,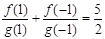 ,若有穷数列
,若有穷数列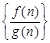 (
(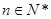 )的前
)的前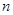 项和等于
项和等于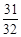 ,则n等于
,则n等于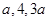 为等差数列的连续三项,则
为等差数列的连续三项,则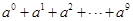 的值为 ( )
的值为 ( )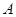
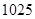
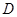
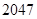
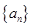 (
(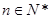 )的前n项和为
)的前n项和为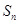 ,该数列是单调递增数列,若
,该数列是单调递增数列,若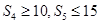 ,则
,则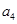 的取值范围是
的取值范围是