题目内容
已知椭圆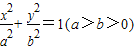 的离心率
的离心率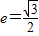 ,连接椭圆的四个顶点得到的菱形的面积为4.
,连接椭圆的四个顶点得到的菱形的面积为4.(1)求椭圆的方程;
(2)设直线l与椭圆相交于不同的两点A,B,已知点A的坐标为(-a,0),点Q(0,y)在线段AB的垂直平分线上,且
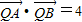 ,求y的值.
,求y的值.
【答案】分析:(1)由离心率求得a和c的关系,进而根据c2=a2-b2求得a和b的关系,进而根据 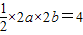 求得a和b,则椭圆的方程可得.
求得a和b,则椭圆的方程可得.
(2)由(1)可求得A点的坐标,设出点B的坐标和直线l的斜率,表示出直线l的方程与椭圆方程联立,消去y,由韦达定理求得点B的横坐标的表达式,进而利用直线方程求得其纵坐标表达式,表示出|AB|进而求得k,则直线的斜率可得.设线段AB的中点为M,当k=0时点B的坐标是(2,0),线段AB的垂直平分线为y轴,进而根据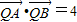 求得y;当k≠0时,可表示出线段AB的垂直平分线方程,令x=0得到y的表达式根据
求得y;当k≠0时,可表示出线段AB的垂直平分线方程,令x=0得到y的表达式根据 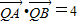 求得y;综合答案可得.
求得y;综合答案可得.
解答:解:(1)由e=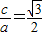 ,得3a2=4c2.
,得3a2=4c2.
再由c2=a2-b2,解得a=2b.
由题意可知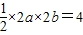 ,即ab=2.
,即ab=2.
解方程组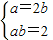 得a=2,b=1.
得a=2,b=1.
所以椭圆的方程为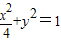 .
.
(2)由(Ⅰ)可知点A的坐标是(-2,0).
设点B的坐标为(x1,y1),直线l的斜率为k.
则直线l的方程为y=k(x+2).
于是A、B两点的坐标满足方程组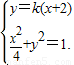
消去y并整理,得(1+4k2)x2+16k2x+(16k2-4)=0.
由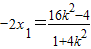 ,得
,得 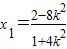 .从而
.从而 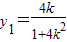 .
.
所以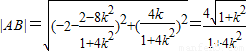 .
.
设线段AB的中点为M,
则M的坐标为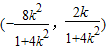 .
.
以下分两种情况:
①当k=0时,点B的坐标是(2,0),
线段AB的垂直平分线为y轴,
于是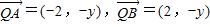 .
.
由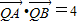 ,得
,得 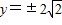 .
.
②当k≠0时,线段AB的垂直平分线方程为
 .
.
令x=0,解得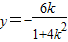 .
.
由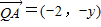 ,
,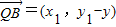 ,
,
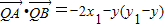
=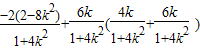
=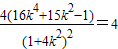 ,
,
整理得7k2=2.故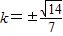 .
.
所以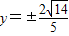 .
.
综上,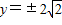 或
或 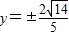 .
.
点评:本小题主要考查椭圆的标准方程和几何性质、直线的方程、两点间的距离公式、直线的倾斜角、平面向量等基础知识,考查用代数方法研究圆锥曲线的性质及数形结合的思想,考查综合分析与运算能力.综合性强,难度大,易出错.
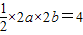 求得a和b,则椭圆的方程可得.
求得a和b,则椭圆的方程可得.(2)由(1)可求得A点的坐标,设出点B的坐标和直线l的斜率,表示出直线l的方程与椭圆方程联立,消去y,由韦达定理求得点B的横坐标的表达式,进而利用直线方程求得其纵坐标表达式,表示出|AB|进而求得k,则直线的斜率可得.设线段AB的中点为M,当k=0时点B的坐标是(2,0),线段AB的垂直平分线为y轴,进而根据
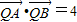 求得y;当k≠0时,可表示出线段AB的垂直平分线方程,令x=0得到y的表达式根据
求得y;当k≠0时,可表示出线段AB的垂直平分线方程,令x=0得到y的表达式根据 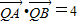 求得y;综合答案可得.
求得y;综合答案可得.解答:解:(1)由e=
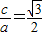 ,得3a2=4c2.
,得3a2=4c2.再由c2=a2-b2,解得a=2b.
由题意可知
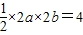 ,即ab=2.
,即ab=2.解方程组
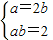 得a=2,b=1.
得a=2,b=1.所以椭圆的方程为
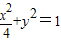 .
.(2)由(Ⅰ)可知点A的坐标是(-2,0).
设点B的坐标为(x1,y1),直线l的斜率为k.
则直线l的方程为y=k(x+2).
于是A、B两点的坐标满足方程组
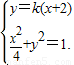
消去y并整理,得(1+4k2)x2+16k2x+(16k2-4)=0.
由
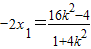 ,得
,得 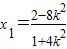 .从而
.从而 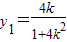 .
.所以
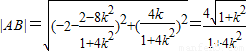 .
.设线段AB的中点为M,
则M的坐标为
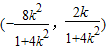 .
.以下分两种情况:
①当k=0时,点B的坐标是(2,0),
线段AB的垂直平分线为y轴,
于是
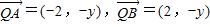 .
.由
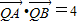 ,得
,得 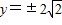 .
.②当k≠0时,线段AB的垂直平分线方程为
 .
.令x=0,解得
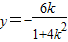 .
.由
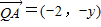 ,
,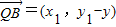 ,
,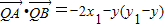
=
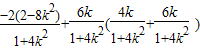
=
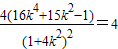 ,
,整理得7k2=2.故
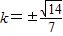 .
.所以
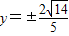 .
.综上,
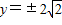 或
或 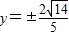 .
.点评:本小题主要考查椭圆的标准方程和几何性质、直线的方程、两点间的距离公式、直线的倾斜角、平面向量等基础知识,考查用代数方法研究圆锥曲线的性质及数形结合的思想,考查综合分析与运算能力.综合性强,难度大,易出错.

练习册系列答案
相关题目

 的离心率为
的离心率为 ,以原点为圆心,椭圆的短半轴为半径的圆与直线
,以原点为圆心,椭圆的短半轴为半径的圆与直线 相切.
相切. 的方程;
的方程; ,
, ,
, 是椭圆
是椭圆 轴对称的任意两个不同的点,连结
轴对称的任意两个不同的点,连结 交椭圆
交椭圆 ,证明直线
,证明直线 与
与 ;
; ,
, 两点,求
两点,求 的取值范围.
的取值范围.
 的离心率为
的离心率为 ,以原点为圆心,椭圆的短半轴为半径的圆与直线
,以原点为圆心,椭圆的短半轴为半径的圆与直线 相切.
相切. 的方程;
的方程; ,
, ,
, 是椭圆
是椭圆 轴对称的任意两个不同的点,连结
轴对称的任意两个不同的点,连结 交椭圆
交椭圆 ,证明直线
,证明直线 与
与 ;
; ,
, 两点,求
两点,求 的取值范围.
的取值范围.