题目内容
3.若-$\frac{2π}{3}$≤θ≤$\frac{π}{6}$,利用三角函数线,可得sinθ的取值范围是[-1,$\frac{1}{2}$].分析 在单位圆内画出对应的正弦函数线,根据正弦线求出-$\frac{2π}{3}$≤θ≤$\frac{π}{6}$时sinθ的取值范围.
解答 解:-$\frac{2π}{3}$≤θ≤$\frac{π}{6}$,在单位圆内画出对应的正弦函数线,如图所示;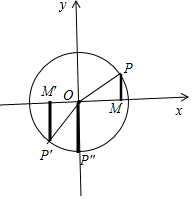
则-$\frac{2π}{3}$对应的正弦线为$\overrightarrow{M′P′}$,正弦值为-$\frac{\sqrt{3}}{2}$;
$\frac{π}{6}$对应的正弦线为$\overrightarrow{PM}$,正弦值为$\frac{1}{2}$,
其中-$\frac{π}{2}$对应的正弦值线为$\overrightarrow{OP″}$,正弦值为-1,
利用三角函数线,可得-$\frac{2π}{3}$≤θ≤$\frac{π}{6}$时,
sinθ的取值范围是[-1,$\frac{1}{2}$].
故答案为:[-1,$\frac{1}{2}$].
点评 本题考查了单位圆与正弦函数线的应用问题,是基础题.

练习册系列答案
相关题目
15.数列{an}是以a为首项,q为公比的等比数列,数列{bn}满足bn=1+a1+a2+…+an(n=1,2,…),数列{cn}满足cn=2+b1+b2+…+bn(n=1,2,…).若{cn}为等比数列,则a+q=( )
| A. | $\sqrt{2}$ | B. | 3 | C. | $\sqrt{5}$ | D. | 6 |
12.已知向量$\overrightarrow{AB}=(2,-1)$,$\overrightarrow{AC}=(-4,1)$,向量$\overrightarrow{BC}$的坐标是( )
| A. | (-6,2) | B. | (6,-2) | C. | (-2,0) | D. | (2,0) |
 的图像,只需将
的图像,只需将 的图像上每一点
的图像上每一点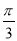 个单位长度
个单位长度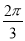 个单位长度
个单位长度
 B.
B. C.
C. D.
D.