题目内容
（1）如图，从相距165m的A、B两观察站测C、D两个目标的视角都是30°，同时知道A在C的正南、B在D的正东，求C、D两个目标间的距离．（2）台湾是祖国不可分割的一部分，祖国的统一是两岸人民共同的愿望，在台湾海峡各自的海域内，当大陆船只与台湾船只相距最近时，两船均相互鸣笛问好，一天，海面上离台湾船只A的正北方向100海里处有一大陆船只B正以每小时20海里的速度沿北偏西60度角的方向行驶，而台湾船只A以每小时15海里的速度向正北方向行驶，若两船同时出发，问几小时后，两船鸣笛问好？
分析：（1）确定A、B、C、D共圆，可得∠ACD=∠ABD，利用正弦定理，即可求得结论；
（2）构造三角形CBD，利用余弦定理，结合配方法，即可得到结论．
（2）构造三角形CBD，利用余弦定理，结合配方法，即可得到结论．
解答：解：（1）由∠DAC=∠DBC=30°，得A、B、C、D共圆，∴∠ACD=∠ABD．
∵
=
，
=
∴
=
∵∠ADB=60°，∴CD=
=55
米；
（2）设x小时后，B船到C处，A传到D处，BC=20x，BD=100-15x＞0，∠CBD=120°，
由余弦定理，可得CD2=400x2+（100-15x）2-2•20x•（100-15x）cos120°
=325（x-
）2+10000-
（0＜x＜
）
所以，当x=
时，两船鸣笛问好．
∵
| CD |
| sin∠DAC |
| AD |
| sin∠ACD |
| AD |
| sin∠ABD |
| AB |
| sin∠ADB |
∴
| CD |
| sin∠DAC |
| AB |
| sin∠ADB |
∵∠ADB=60°，∴CD=
| 165•sin30° |
| sin60° |
| 3 |
（2）设x小时后，B船到C处，A传到D处，BC=20x，BD=100-15x＞0，∠CBD=120°，
由余弦定理，可得CD2=400x2+（100-15x）2-2•20x•（100-15x）cos120°
=325（x-
| 20 |
| 13 |
| 10000 |
| 13 |
| 20 |
| 3 |
所以，当x=
| 20 |
| 13 |
点评：本题考查正弦定理、余弦定理的运用，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
鹰派教辅衔接教材河北教育出版社系列答案
初中暑期衔接系列答案
相关题目
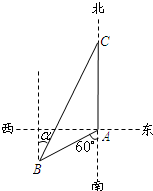如图，渔船甲位于岛屿A的南偏西60°方向的B处，且与岛屿A相距12海里，渔船乙以10海里/小时的速度从岛屿A出发沿正北方向航行，若渔船甲同时从B处出发沿北偏东α的方向追赶渔船乙，刚好用2小时追上．
如图，一架飞机原计划从空中A处直飞相距680km的空中B处，为避开直飞途中的雷雨云层，飞机在A处沿与原飞行方向成θ角的方向飞行，在中途C处转向与原方向线成45°角的方向直飞到达B处．已
（1）如图，从相距165m的A、B两观察站测C、D两个目标的视角都是30°，同时知道A在C的正南、B在D的正东，求C、D两个目标间的距离．
