题目内容
对于函数 ,如果存在区间
,如果存在区间 ,同时满足下列条件:①
,同时满足下列条件:① 在
在 内是单调的;②当定义域是
内是单调的;②当定义域是 时,
时, 的值域也是
的值域也是 ,则称
,则称 是该函数的“和谐区间”.若函数
是该函数的“和谐区间”.若函数 存在“和谐区间”,则
存在“和谐区间”,则 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
B
解析试题分析:依题意可得. 存在“和谐区间”所以f(x)在区间上是单调即x<0或x>0.由于f(x)在x<0上递增,在x>0上递增.在此仅考虑x>0的情况.依题意可得
存在“和谐区间”所以f(x)在区间上是单调即x<0或x>0.由于f(x)在x<0上递增,在x>0上递增.在此仅考虑x>0的情况.依题意可得 即
即 .即函数
.即函数 存在两个大于零的实根.又因为
存在两个大于零的实根.又因为 .所以只需要
.所以只需要 .又因为
.又因为 .所以
.所以 .故选B.理解和谐函数的含义是关键.由两个方程抽象出一个二次方程的根这个思想要理解.
.故选B.理解和谐函数的含义是关键.由两个方程抽象出一个二次方程的根这个思想要理解.
考点:1.新定义问题.2.函数的单调性.3.二次方程根的两个根的问题的含义.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
已知函数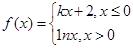 ,若
,若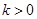 ,则函数
,则函数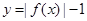 的零点个数是( )
的零点个数是( )
| A.1 | B.2 | C.3 | D.4 |
下列函数中,在定义域上既是奇函数又是增函数的为( )
A. | B. | C. | D. |
下列函数中既是偶函数又在(0,+∞)上是增函数的是( )
A.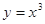 | B.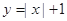 | C.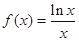 | D.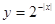 |
已知函数 ,则
,则 ( )
( )
| A.0 | B.2 | C.-2 | D.4 |
设集合A=B=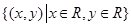 ,从A到B的映射
,从A到B的映射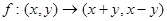 在映射下,B中的元素为(4,2)对应的A中元素为 ( )
在映射下,B中的元素为(4,2)对应的A中元素为 ( )
| A.(4,2) | B.(1,3) | C.(6,2) | D.(3,1) |
设函数 ,集合
,集合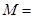
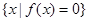 =
=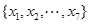
 ,设
,设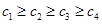 ,则
,则
| A.9 | B.8 | C.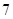 | D.6 |
 是定义在
是定义在 上的奇函数,若对于任意的实数
上的奇函数,若对于任意的实数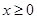 ,都有
,都有 ,且当
,且当 时,
时, ,则
,则 的值为( )
的值为( )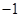



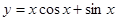 的图像大致为( )
的图像大致为( )