题目内容
、(本题15分)已知函数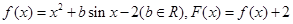 ,且对于任意实数
,且对于任意实数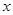 ,恒有F(x)=F(-x)。(1)求函数
,恒有F(x)=F(-x)。(1)求函数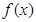 的解析式;
的解析式;
(2)已知函数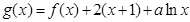 在区间
在区间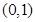 上单调,求实数
上单调,求实数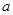 的取值范围;
的取值范围;
(3)函数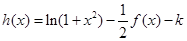 有几个零点?
有几个零点?
【答案】
解:(1)由题设得 ,
,
 ,则
,则 ,
,
所以
所以 对于任意实数
对于任意实数 恒成立
恒成立
 .故
.故 . ……………………………………………………4分(2)由
. ……………………………………………………4分(2)由 ,求导数得
,求导数得
 ,
, 在
在 上恒单调,只需
上恒单调,只需 或
或 在
在 上恒成立,即
上恒成立,即 或
或 恒成立,
恒成立,
所以 或
或 在
在 上恒成立.
上恒成立.
记 ,可知:
,可知: ,
,
 或
或 . ……………………………………………………………………9分(3)令
. ……………………………………………………………………9分(3)令 ,则
,则 .
.
令 ,则
,则 ,列表如下.
,列表如下.
|
|
|
|
|
0 |
|
1 |
|
|
|
+ |
0 |
— |
0 |
+ |
0 |
— |
|
|
递增 |
极大值 |
递减 |
极小值1 |
递增 |
极大值 |
递减 |

 时,无零点;
时,无零点;
 或
或
 时,有两个零点;
时,有两个零点;
 时有三个零点;
时有三个零点;
 时,有四个零点. ……………………………………………………15分
时,有四个零点. ……………………………………………………15分
【解析】略

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目








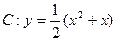 ,点
,点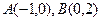 ,点E是曲线C上的一个动点(E不在直线AB上),设
,点E是曲线C上的一个动点(E不在直线AB上),设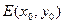 ,C,D在直线AB上,
,C,D在直线AB上,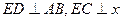 轴。
轴。 表示
表示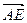 在
在 方向上的投影;
方向上的投影;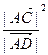 是否为定值?若是,求此定值,若不是,说明理由。
是否为定值?若是,求此定值,若不是,说明理由。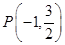 是椭圆E:
是椭圆E: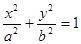 (
(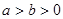 )上一点,F1、F2分别是椭圆E的左、右焦点,O是坐标原点,PF1⊥x轴.
)上一点,F1、F2分别是椭圆E的左、右焦点,O是坐标原点,PF1⊥x轴.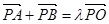 (
(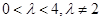 ).求证:直线AB的斜率为定值;
).求证:直线AB的斜率为定值;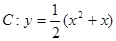 ,点
,点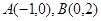 ,点E是曲线C上的一个动点(E不在直线AB上),设
,点E是曲线C上的一个动点(E不在直线AB上),设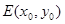 ,C,D在直线AB上,
,C,D在直线AB上,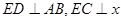 轴。
轴。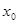 表示
表示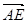 在
在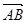 方向上的投影;
方向上的投影;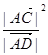 是否为定值?若是,求此定值,若不是,说明理由。
是否为定值?若是,求此定值,若不是,说明理由。