题目内容
已知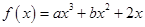 在
在 处取得极值,且在点
处取得极值,且在点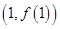 处的切线斜率为
处的切线斜率为 .
.
⑴求 的单调增区间;
的单调增区间;
⑵若关于 的方程
的方程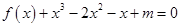 在区间
在区间 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数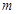 的取值范围.
的取值范围.
(1)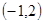 ;(2)
;(2)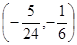
解析试题分析:(1)要求高次函数的单调增区间,只能使用导数法,令 ,解得其增区间.所以得确定其函数解析式.根据导数的几何意义知
,解得其增区间.所以得确定其函数解析式.根据导数的几何意义知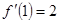 ,根据在
,根据在 处取得极值,可知
处取得极值,可知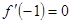 ,解方程组可得
,解方程组可得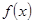 解析式.
解析式.
(2)构造新函数 ,根据其在区间
,根据其在区间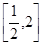 上有两个不等的实数根,可知新函数在该区间内与
上有两个不等的实数根,可知新函数在该区间内与 轴有两个不同的交点.根据新函数在该区间内的单调性以及极值建立关系式,解决;
轴有两个不同的交点.根据新函数在该区间内的单调性以及极值建立关系式,解决;
试题解析:⑴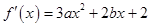 1分;由题意,得
1分;由题意,得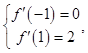
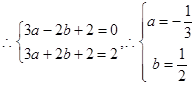 3分
3分 ,由
,由 得
得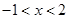 ;
;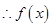 的单调增区间是
的单调增区间是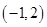 5分
5分
⑵由⑴知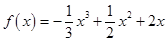 ;
;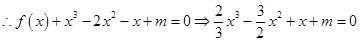 ;
;
令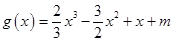 ;
;
则 ,由
,由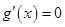 得
得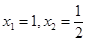 7分;
7分;
当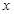 变化时,
变化时,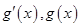 的变化情况如下表:
的变化情况如下表: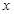
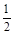
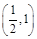
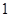


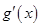
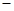
0 + 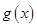
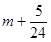


极小值 
 练习册系列答案
练习册系列答案
分层学习检测与评价系列答案
普通高中招生考试命题指导纲要系列答案
高分计划系列答案
高效测评单元测评系列答案
高效测评小学升学全真模拟试卷系列答案
高效复习系列答案
高效课堂小升初毕业总复习系列答案
高效期末复习系列答案
高效期末卷系列答案
高中数学知识方法和实践系列答案
相关题目
 ,其中
,其中 .
.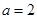 时,求函数
时,求函数 的图象在点
的图象在点 处的切线方程;
处的切线方程;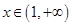 ,都有
,都有 ,求
,求 的取值范围.
的取值范围. ,当
,当 时,
时,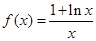 .
.
 上存在极值点,求实数a的取值范围;
上存在极值点,求实数a的取值范围; 时,不等式
时,不等式 恒成立,求实数k的取值范围;
恒成立,求实数k的取值范围;
 .
. .
. ,求
,求 的解析式;
的解析式; 在
在 上恒成立,求实数
上恒成立,求实数 的取值范围;
的取值范围; .
.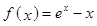 (e为自然对数的底数)
(e为自然对数的底数)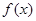 的最小值;
的最小值;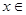
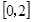 ,不等式
,不等式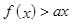 恒成立,求实数
恒成立,求实数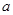 的取值范围.
的取值范围.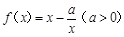 ,
, ,且直线
,且直线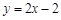 与曲线
与曲线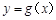 相切.
相切.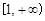 内的一切实数
内的一切实数 ,不等式
,不等式 恒成立,求实数
恒成立,求实数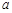 的取值范围;
的取值范围;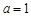 时,求最大的正整数
时,求最大的正整数 ,使得对
,使得对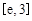 (
(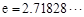 是自然对数的底数)内的任意
是自然对数的底数)内的任意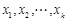 都有
都有 成立;
成立; .
.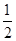 s~6 s间的运动路程.
s~6 s间的运动路程.