题目内容
(04年天津卷理)(14分)
椭圆的中心是原点O,它的短轴长为![]() ,相应于焦点
,相应于焦点![]() 的准线
的准线![]() 与
与![]() 轴相交于点A,
轴相交于点A,![]() ,过点A的直线与椭圆相交于P、Q两点。
,过点A的直线与椭圆相交于P、Q两点。
(I) 求椭圆的方程及离心率;
(II)若![]() 求直线PQ的方程;
求直线PQ的方程;
(III)设![]() ,过点P且平行于准线
,过点P且平行于准线![]() 的直线与椭圆相交于另一点M,证明
的直线与椭圆相交于另一点M,证明
![]() 。
。
解析:(I)解:由题意,可设椭圆的方程为![]()
由已知得
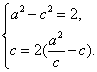
解得 ![]()
所以椭圆的方程为![]() ,离心率
,离心率![]() 。。。。。。。。。。。4分
。。。。。。。。。。。4分
(II)解: 由(I)可得![]()
设直线PQ的方程为![]() 由方程组
由方程组
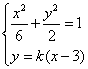
得 ![]()
依题意 ![]() 得
得
![]()
设 ![]() 则
则
![]() ①
①
![]() ②
②
由直线PQ的方程得 ![]() 于是
于是
![]() ③
③
![]() ④ 。。。。。。。。。。。。。。8分
④ 。。。。。。。。。。。。。。8分
由①②③④得![]() 从而
从而![]()
所以直线PQ的方程为
![]() 或
或![]() 。。。。。。。。。。。。。10分
。。。。。。。。。。。。。10分
(III)证明:![]() 由已知得方程组
由已知得方程组
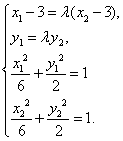
注意![]() 解得
解得 ![]() 。。。。。。。。。。。。。。。。。。。。。12分
。。。。。。。。。。。。。。。。。。。。。12分
因![]() 故
故
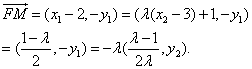
而![]() 所以
所以
![]() 。。。。。。。。。。。。。。。。。。14分
。。。。。。。。。。。。。。。。。。14分

练习册系列答案
相关题目
