题目内容
5.已知数列{an}满足:${a_1}=2,{a_{n+1}}+{a_n}=9×{2^{n-1}}$.(1)记${b_n}={a_n}-3×{2^{n-1}}$,求证:数列{bn}为等比数列;
(2)求数列{nan}的前n项和Sn.
分析 (1)数列{an}满足:${a_1}=2,{a_{n+1}}+{a_n}=9×{2^{n-1}}$.变形为${a}_{n+1}-3×{2}^{n}$=-$({a}_{n}-3×{2}^{n-1})$,由${b_n}={a_n}-3×{2^{n-1}}$,可得:bn+1=-bn,利用等比数列的定义即可证明;
(2)由(1)可知:bn=(-1)n,即an=3×2n-1+(-1)n,$n{a_n}=3n×{2^{n-1}}+n×{(-1)^n}$,利用“错位相减法”、分类讨论与分组求和即可得出.
解答 (1)证明:数列{an}满足:${a_1}=2,{a_{n+1}}+{a_n}=9×{2^{n-1}}$.变形为${a}_{n+1}-3×{2}^{n}$=-$({a}_{n}-3×{2}^{n-1})$,由${b_n}={a_n}-3×{2^{n-1}}$,可得:bn+1=-bn,
其中b1=a1-3=-1,∴数列{bn}为等比数列,首项与公比都为-1.
(2)解:由(1)可知:bn=(-1)n,即an=3×2n-1+(-1)n.
∴$n{a_n}=3n×{2^{n-1}}+n×{(-1)^n}$,…(6分)
设${T_n}=1×{2^0}+2×{2^1}+3×{2^2}+…+(n-1)×{2^{n-2}}+n×{2^{n-1}}$,①
$2{T_n}=1×{2^1}+2×{2^2}+3×{2^3}+…+(n-1)×{2^{n-1}}+n×{2^n}$,②
①-②得$-{T_n}={2^0}+{2^1}+{2^2}+…+{2^{n-1}}-n×{2^n}={2^n}-1-n×{2^n}$,
∴${T_n}=1+(n-1)×{2^n}$,…(8分)
设${Q_n}=-1+2-3+…+{(-1)^n}n$,即${Q_n}=\left\{{\begin{array}{l}{-\frac{n+1}{2},\;n为奇数}\\{\frac{n}{2},\;n为偶数}\end{array}}\right.$,…(10分)
∴${S_n}=3{T_n}+{Q_n}=\left\{{\begin{array}{l}{3(n-1)×{2^n}-\frac{n-5}{2},n为奇数}\\{3(n-1)×{2^n}+\frac{n+6}{2},\;n为偶数}\end{array}}\right.$,…(12分)
点评 本题考查了递推关系、等比数列的通项公式及其前n项和公式、“错位相减法”与分组求和方法、分类讨论方法,考查了推理能力与计算能力,属于中档题.

 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案| A. | $\frac{2\sqrt{3}}{3}$ | B. | $\frac{2\sqrt{2}}{3}$ | C. | $\frac{\sqrt{2}}{4}$ | D. | $\frac{3\sqrt{2}}{4}$ |

| A. | -1 | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
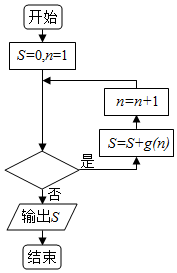 已知函数f(x)=ax3+$\frac{1}{2}$x2在x=-1处取得极大值,记g(x)=$\frac{1}{f′(x)}$.在如图所示的程序框图中,若输出的结果S=$\frac{2016}{2017}$,则判断框中可以填入的关于n的判断条件是( )
已知函数f(x)=ax3+$\frac{1}{2}$x2在x=-1处取得极大值,记g(x)=$\frac{1}{f′(x)}$.在如图所示的程序框图中,若输出的结果S=$\frac{2016}{2017}$,则判断框中可以填入的关于n的判断条件是( )| A. | n≤2016? | B. | n≤2017? | C. | n>2016? | D. | n>2017? |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |