题目内容
若直三棱柱ABC-A1B1C1的所有顶点都在球O的球面上,AA1=2
,AB=1,AC=2,∠ABC=90°,则球O的表面积为
| 3 |
16π
16π
.分析:由于直三棱柱ABC-A1B1C1的底面ABC为等腰直角三角形,我们可以把直三棱柱ABC-A1B1C1补成四棱柱,则四棱柱的体对角线是其外接球的直径,求出外接球的直径后,代入外接球的表面积公式,即可求出该三棱柱的外接球的表面积.
解答: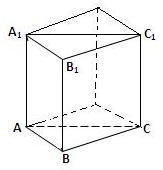 解:由于直三棱柱ABC-A1B1C1的底面ABC为等腰直角三角形,
解:由于直三棱柱ABC-A1B1C1的底面ABC为等腰直角三角形,
把直三棱柱ABC-A1B1C1补成四棱柱,
则四棱柱的体对角线是其外接球的直径,
所以外接球半径为
=2,
则三棱柱ABC-A1B1C1外接球的表面积是4πR2=16π.
故答案为:16π.
 解:由于直三棱柱ABC-A1B1C1的底面ABC为等腰直角三角形,
解:由于直三棱柱ABC-A1B1C1的底面ABC为等腰直角三角形,把直三棱柱ABC-A1B1C1补成四棱柱,
则四棱柱的体对角线是其外接球的直径,
所以外接球半径为
| 1 |
| 2 |
12+(
|
则三棱柱ABC-A1B1C1外接球的表面积是4πR2=16π.
故答案为:16π.
点评:本题考查球的体积和表面积,球的内接体问题,考查学生空间想象能力,是基础题.

练习册系列答案
相关题目
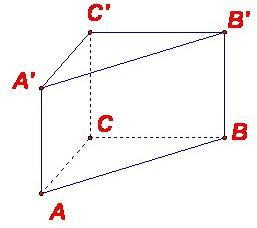 如图,在直三棱柱ABC-A′B′C′中,CC′=AC=BC=2,∠ACB=90°.
如图,在直三棱柱ABC-A′B′C′中,CC′=AC=BC=2,∠ACB=90°.
 (2012•辽宁)如图,直三棱柱ABC-A'B'C',∠BAC=90°,AB=AC=λAA',点M,N分别为A'B和B'C'的中点.
(2012•辽宁)如图,直三棱柱ABC-A'B'C',∠BAC=90°,AB=AC=λAA',点M,N分别为A'B和B'C'的中点. 如图,在直三棱柱ABC-A′B′C′中,AA′=AB=BC=1,∠ABC=90°.棱A′C′上有两个动点E,F,且EF=a (a为常数).
如图,在直三棱柱ABC-A′B′C′中,AA′=AB=BC=1,∠ABC=90°.棱A′C′上有两个动点E,F,且EF=a (a为常数).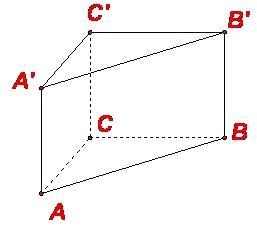 如图,在直三棱柱ABC-A′B′C′中,CC′=AC=BC=2,∠ACB=90°.
如图,在直三棱柱ABC-A′B′C′中,CC′=AC=BC=2,∠ACB=90°.