题目内容
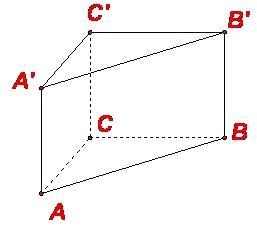如图，在直三棱柱ABC-A′B′C′中，CC′=AC=BC=2，∠ACB=90°．
（1）如图给出了该直三棱柱三视图中的正视图，请根据此画出它的侧视图和俯视图；
（2）若P是AA′的中点，求四棱锥B′-C′A′PC的体积；
（3）求A′B与平面CB′所成角的正切值．
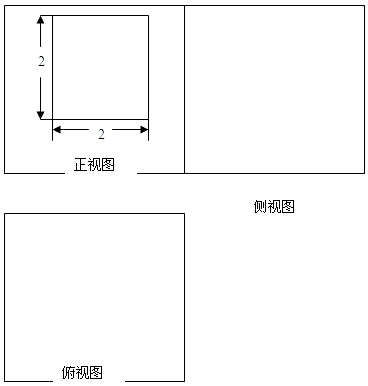
解：（1）
；
（2）由题意可知，底面面积为：3，所以四棱锥B′-C′A′PC的体积V=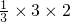
=2；
（3）连接C′B，则A′B与平面CB′所成角的正切值为：
=
．
分析：（1）根据三视图的作法，直接画出正视图和俯视图即可．
（2）根据三视图的数据关系，求出几何体的底面面积和高，求出棱锥的体积．
（3）作出A′B与平面CB′所成角，然后解三角形求出A′B与平面CB′所成角的正切值．
点评：本题是中档题，考查直线与平面所成角正切值的求法，棱锥的体积的求法，考查计算能力，三视图的作法，熟练掌握基本定理、基本方法是解决本题的关键．
；（2）由题意可知，底面面积为：3，所以四棱锥B′-C′A′PC的体积V=
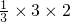=2；（3）连接C′B，则A′B与平面CB′所成角的正切值为：
=．分析：（1）根据三视图的作法，直接画出正视图和俯视图即可．
（2）根据三视图的数据关系，求出几何体的底面面积和高，求出棱锥的体积．
（3）作出A′B与平面CB′所成角，然后解三角形求出A′B与平面CB′所成角的正切值．
点评：本题是中档题，考查直线与平面所成角正切值的求法，棱锥的体积的求法，考查计算能力，三视图的作法，熟练掌握基本定理、基本方法是解决本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
