题目内容
(本小题满分14分)如图,在直角梯形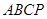 中,
中,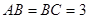 ,
,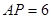 ,
,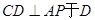 ,现将
,现将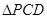 沿线段
沿线段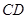 折成
折成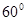 的二面角
的二面角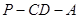 ,设
,设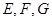 分别是
分别是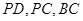 的中点.
的中点.
(Ⅰ) 求证: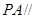 平面
平面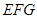 ;
;
(II)若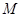 为线段
为线段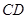 上的动点,问点
上的动点,问点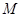 在什么位置时,
在什么位置时,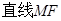 与平面
与平面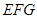 所成角为
所成角为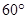 .
.

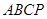 中,
中,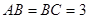 ,
,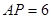 ,
,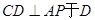 ,现将
,现将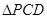 沿线段
沿线段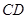 折成
折成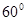 的二面角
的二面角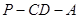 ,设
,设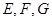 分别是
分别是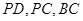 的中点.
的中点.(Ⅰ) 求证:
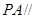 平面
平面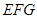 ;
;(II)若
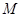 为线段
为线段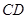 上的动点,问点
上的动点,问点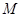 在什么位置时,
在什么位置时,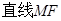 与平面
与平面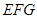 所成角为
所成角为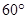 .
.
(Ⅰ)证明:取
 中点
中点 ,连接
,连接 ,
, ,
,易得四边形
 为梯形,有
为梯形,有 在平面
在平面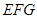 上,又
上,又 ,
, 结合
 平面
平面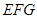 ,
, 平面
平面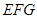 ,得
,得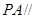 平面
平面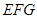 ;……………………6分
;……………………6分(Ⅱ)分别以
 ,
, ,
, 为
为 轴,
轴, 轴,
轴, 轴,建立空间直角坐标系
轴,建立空间直角坐标系 ,有
,有 ,
, .
. 设平面
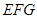 的法向量为
的法向量为 ,则根据
,则根据
 ,取
,取 ,得到
,得到 .
. 设点

 ,于是
,于是 ,
, 有题知
 ,
, 即
 ,解得
,解得 .
. ∴点
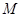 在
在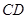 的中点时,
的中点时, 与平面
与平面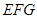 所成角为
所成角为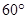 .…………………………14分
.…………………………14分略

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
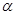 是空间中的一个平面,
是空间中的一个平面,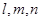 是三条不同的直线,
是三条不同的直线, 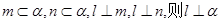 ; ②若
; ②若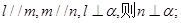
 ,则
,则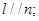 ④若
④若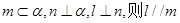 ;
;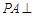 矩形
矩形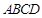 所在平面,
所在平面,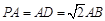 ,
,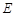 为线段
为线段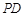 上一点,
上一点,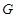 为线段
为线段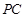
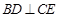 ;
;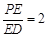 时,求证:BG//平面AEC.
时,求证:BG//平面AEC.
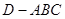 中,
中,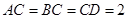 ,
, 平面
平面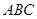 ,
, 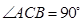 . 若其主视图,俯视图如图所示,则其左视图的面积为( )
. 若其主视图,俯视图如图所示,则其左视图的面积为( )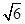
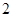
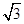
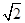
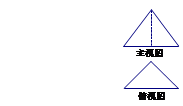
 中(图1),
中(图1), 是
是 的中点,
的中点, ,
,
 ,
, 将(图1)沿直线
将(图1)沿直线 折起,使二面角
折起,使二面角 为
为 (如图2)
(如图2) 平面
平面 ;
; 与
与 所成角的余弦值;
所成角的余弦值; 到平面
到平面 的距离.
的距离.
 平面ABCD,
平面ABCD, ABC=60O,E,F分别是BC,PC
ABC=60O,E,F分别是BC,PC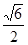 。
。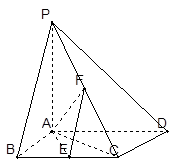
 中,
中, ,
, ,
, ,
, 为
为 上的点,若
上的点,若 ,则
,则 ____________(结果用反三角表示).
____________(结果用反三角表示).