题目内容
一台机器使用的时间较长,但还可以使用,它按不同的转速生产出来的某机械零件有一些会有缺点,每小时生产有缺点零件的多少,随机器的运转的速度而变化,下表为抽样试验的结果:| 转速x(转/秒) | 16 | 14 | 12 | 8 |
| 每小时生产有缺点的零件数y(件) | 11 | 9 | 8 | 5 |
(2)如果y对x有线性相关关系,求回归直线方程;
(3)若实际生产中,允许每小时的产品中有缺点的零件最多为10个,那么机器的运转速度应控制在什么范围内?(最后结果精确到0.001.参考数据:
| 656.25 |
分析:(1)利用所给的数据做出两个变量的相关系数,得到相关系数趋近于1,得到两个变量具有线性相关关系.
(2)先做出横标和纵标的平均数,做出利用最小二乘法求线性回归方程的系数的量,做出系数,求出a,写出线性回归方程.
(3)根据上一问做出的线性回归方程,使得函数值小于或等于10,解出不等式.
(2)先做出横标和纵标的平均数,做出利用最小二乘法求线性回归方程的系数的量,做出系数,求出a,写出线性回归方程.
(3)根据上一问做出的线性回归方程,使得函数值小于或等于10,解出不等式.
解答:解:(1)
=12.5,
=8.25,
(xi-
)(yi-
)=25.5
=
≈25.617
∴r≈0.995>0.75,y与x有线性性相关关系.
(2)
(xi-
)2=35
∴
=0.728571,
=
-
=-0.857138
∴回归直线方程为:y=0.729x-0.857
(3)由上一问可知0.729x-0.857≤10,
解得x≤14.893
. |
| x |
. |
| y |
| n |
 |
| i=1 |
. |
| x |
. |
| y |
|
| 656.25 |
∴r≈0.995>0.75,y与x有线性性相关关系.
(2)
| n |
 |
| i=1 |
. |
| x |
∴
| ? |
| b |
| ? |
| a |
. |
| y |
| ? |
| b |
. |
| x |
∴回归直线方程为:y=0.729x-0.857
(3)由上一问可知0.729x-0.857≤10,
解得x≤14.893
点评:本题考查线性回归方程的求法和应用,是一个近几年新课标出现的题目,本题解题的关键是数字的计算要细心.

练习册系列答案
相关题目
一台机器使用的时间较长,但还可以使用,它按不同的转速生产出来的某机械零件有一些会有缺点,每小时生产有缺点零件的多少,随机器的运转的速度而变化,下表为抽样试验的结果:
|
转速x(转/秒) |
16 |
14 |
12 |
8 |
|
每小时生产有缺点的零件数y(件) |
11 |
9 |
8 |
5 |
画出散点图,并通过散点图确定变量y对x是否线性相关;
(2)如果y对x有线性相关关系,求回归直线方程;
(3)若实际生产中,允许每小时的产品中有缺点的零件最多为10个,那么机器的运转速度应控制在什么范围内?(精确到0.0001)
一台机器使用的时间较长,但还可以使用,它按不同的转速生产出来的某机械零件有一些会有缺点,每小时生产有缺点零件的多少,随机器的运转的速度而变化,下表为抽样试验的结果:
|
转速x(转/秒) |
2 |
4 |
5 |
6 |
8 |
|
每小时生产有缺点的零件数y(件) |
30 |
40 |
60 |
50 |
70 |
(Ⅰ)画出散点图;
(Ⅱ)如果y对x有线性相关关系,求回归直线方程;
(Ⅲ)若实际生产中,允许每小时的产品中有缺点的零件最多为89个,那么机
器的运转速度应控制在什么范围内?(参考数值: ,
,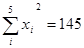 )
)
