题目内容
已知数列 满足:
满足: (其中常数
(其中常数 ).
).
(1)求数列 的通项公式;
的通项公式;
(2)当 时,数列
时,数列 中是否存在不同的三项组成一个等比数列;若存在,求出满足条件的三项,若不存在,说明理由。
中是否存在不同的三项组成一个等比数列;若存在,求出满足条件的三项,若不存在,说明理由。
(1)
(2)不存在这样的正整数 ,使得
,使得 成等比数列.
成等比数列.
解析试题分析:解:(1)当 时,
时, ,
,
当 时,因为
时,因为
所以:
两式相减得到: ,即
,即 ,又
,又 ,
,
所以数列 的通项公式是
的通项公式是 ;
;
(2)当 时,
时, ,假设存在
,假设存在 成等比数列,
成等比数列,
则 .
.
整理得 .
.
由奇偶性知 r+t-2s=0.
r+t-2s=0.
所以 ,即
,即 ,这与
,这与 矛盾,
矛盾,
故不存在这样的正整数 ,使得
,使得 成等比数列.
成等比数列.
考点:数列的通项公式,等比数列
点评:主要是考查了数列的通项公式以及等比数列的定义的运用,属于基础题。

练习册系列答案
相关题目
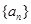 是公比为q的等比数列.
是公比为q的等比数列. 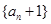 不是等比数列.
不是等比数列. 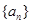 中,
中,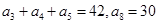 .
.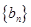 满足
满足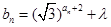 (
( ),则是否存在这样的实数
),则是否存在这样的实数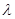 使得
使得 满足
满足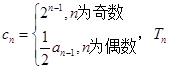 为数列
为数列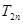 .
.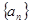 前
前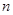 项和
项和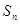 满足
满足 且
且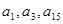 成等比数列,求
成等比数列,求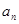 .
.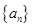 满足
满足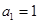 ,
,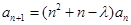 (
(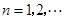 ),
),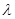 是常数.
是常数.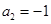 时,求
时,求 的值;
的值; 中,
中, .
. ,求数列
,求数列 的通项公式;
的通项公式; 求证:
求证: .
. 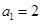 ,点
,点 在函数
在函数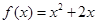 的图象上,其中
的图象上,其中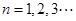
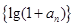 是等比数列,并求数列
是等比数列,并求数列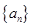 的通项公式;
的通项公式;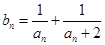 ,求数列
,求数列 的前
的前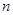 项和
项和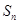 .
. 的前
的前 项和
项和 ,且满足
,且满足 .
. 的值,猜想
的值,猜想 是数列
是数列 的前
的前 .
. tan x+1=0在x
tan x+1=0在x [0,n
[0,n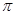 )( n
)( n bn,求实数k的取值范围.
bn,求实数k的取值范围.