题目内容
3.在直角坐标系xOy中,以原点O为极点,x轴的正半轴为极轴建立极坐标系,已知曲线C1的极坐标方程为ρ2=$\frac{3}{1+2co{s}^{2}θ}$,直线l的极坐标方程为ρ=$\frac{4}{sinθ+cosθ}$.(1)写出曲线C1与直线l的直角坐标方程;
(2)设Q为曲线C1上一动点,求Q点到直线l的距离的最小值.
分析 (1)展开把$\left\{\begin{array}{l}{x=ρcosθ}\\{y=ρsinθ}\\{{ρ}^{2}={x}^{2}+{y}^{2}}\end{array}\right.$代入可得直角坐标方程.
(2)设与直线l平行且与曲线C1相切的直线方程为:x+y+m=0,与椭圆方程联立化为:4x2+2mx+m2-3=0,令△=0,解得m,再利用点到直线的距离公式即可得出.
解答 解:(1)曲线C1的极坐标方程为ρ2=$\frac{3}{1+2co{s}^{2}θ}$,化为ρ2+2(ρcosθ)2=3,可得直角坐标方程:x2+y2+2x2=3,即3x2+y2=3.
直线l的极坐标方程为ρ=$\frac{4}{sinθ+cosθ}$,化为ρcosθ+ρsinθ=4,化为直角坐标方程:x+y-4=0.
(2)设与直线l平行且与曲线C1相切的直线方程为:x+y+m=0,
联立$\left\{\begin{array}{l}{x+y+m=0}\\{3{x}^{2}+{y}^{2}=3}\end{array}\right.$,化为:4x2+2mx+m2-3=0,
令△=4m2-16(m2-3)=0,解得m=±2.取切线x+y-2=0.
直线l与切线的距离d=$\frac{|-2-(-3)|}{\sqrt{2}}$=$\frac{\sqrt{2}}{2}$.
∴Q点到直线l的距离的最小值为$\frac{\sqrt{2}}{2}$.
点评 本题考查了极坐标方程与直角坐标方程的互化、直线与椭圆相切问题、点到直线的距离公式、平行线之间的距离,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.若|$\overrightarrow{e}$|=1,且$\overrightarrow{a}⊥\overrightarrow{e}$,|$\overrightarrow{a}$|=2,则|4$\overrightarrow{a}-\overrightarrow{e}$|=( )
| A. | $\sqrt{37}$ | B. | $\sqrt{65}$ | C. | 8 | D. | $\sqrt{13}$ |
6.随机变量ξ服从正态分布N(2,σ2),P(ξ≤4)=0.84,则P(ξ<0)=( )
| A. | 0.16 | B. | 0.32 | C. | 0.68 | D. | 0.84 |
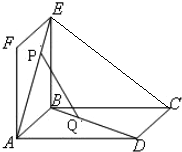 如图:已知有公共边AB的两个全等的矩形ABCD和ABEF不在同一个平面内,P,Q分别是对角线AE,BD上的点,且AP=DQ,求证:PQ∥面CBE.
如图:已知有公共边AB的两个全等的矩形ABCD和ABEF不在同一个平面内,P,Q分别是对角线AE,BD上的点,且AP=DQ,求证:PQ∥面CBE.