题目内容
如图,已知椭圆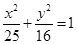 的右焦点为
的右焦点为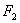 ,点
,点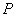 是椭圆上任意一点,圆
是椭圆上任意一点,圆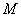 是以
是以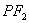 为直径的圆.
为直径的圆.
(1)若圆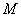 过原点
过原点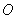 ,求圆
,求圆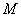 的方程;
的方程;
(2)写出一个定圆的方程,使得无论点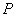 在椭圆的什么位置,该定圆总与圆
在椭圆的什么位置,该定圆总与圆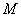 相切,请写出你的探究过程.
相切,请写出你的探究过程.
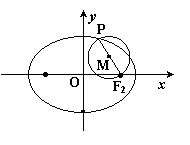
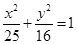 的右焦点为
的右焦点为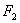 ,点
,点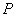 是椭圆上任意一点,圆
是椭圆上任意一点,圆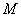 是以
是以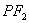 为直径的圆.
为直径的圆.(1)若圆
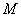 过原点
过原点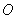 ,求圆
,求圆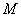 的方程;
的方程; (2)写出一个定圆的方程,使得无论点
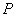 在椭圆的什么位置,该定圆总与圆
在椭圆的什么位置,该定圆总与圆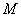 相切,请写出你的探究过程.
相切,请写出你的探究过程. 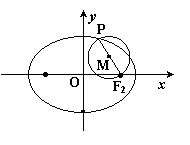
(1)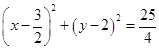 或
或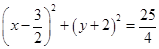 ;(2)
;(2)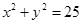 .
.
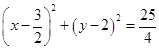 或
或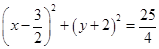 ;(2)
;(2)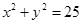 .
.试题分析:(1)因为
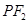 是圆
是圆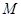 的直径,所以当圆
的直径,所以当圆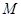 过原点
过原点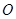 时,一定有
时,一定有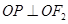 ,由此可确定点
,由此可确定点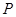 的位置并进一步求出圆
的位置并进一步求出圆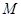 的标准方程;
的标准方程;(2)设圆M的半径为
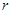 ,连结
,连结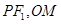 ,显然有
,显然有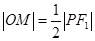
根据椭圆的标准方程
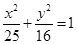 知
知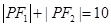 ,
,所以
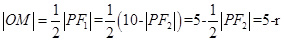
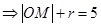 ,从而找到符合条件的定圆.
,从而找到符合条件的定圆.解:(1)解法一:因为圆
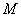 过原点
过原点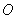 ,所以
,所以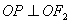 ,所以
,所以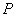 是椭圆的短轴顶点,
是椭圆的短轴顶点,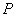 的坐标是
的坐标是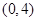 或
或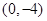 ,于是点
,于是点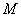 的坐标为
的坐标为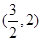 或
或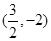 ,
, 易求圆
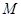 的半径为
的半径为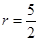
所以圆
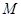 的方程为
的方程为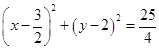 或
或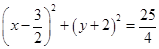 6分
6分解法二:设
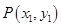 ,因为圆
,因为圆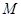 过原点
过原点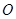 ,所以
,所以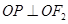
所以
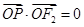 ,所以
,所以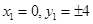 ,所以点
,所以点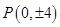
于是点
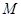 的坐标为
的坐标为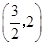 或
或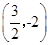 ,易求圆的半径
,易求圆的半径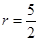
所以圆
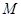 的方程为
的方程为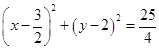 或
或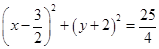 6分
6分(2)以原点为圆心,5为半径的定圆始终与圆相内切,定圆的方程为
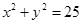 8分
8分探究过程为:设圆
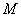 的半径为
的半径为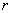 ,定圆的半径为
,定圆的半径为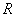 ,
, 因为
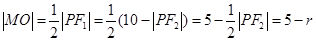 ,
,所以当原点为定圆圆心,半径
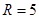 时,定圆始终与圆
时,定圆始终与圆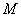 相内切. (13分)
相内切. (13分)
练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
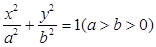 经过点
经过点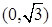 ,离心率为
,离心率为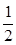 ,左右焦点分别为
,左右焦点分别为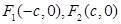 .
.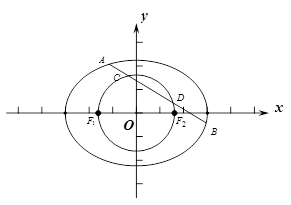
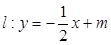 与椭圆交于
与椭圆交于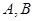 两点,与以
两点,与以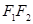 为直径的圆交于
为直径的圆交于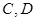 两点,且满足
两点,且满足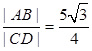 ,求直线
,求直线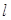 的方程.
的方程.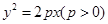 的焦点为F,直线
的焦点为F,直线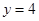 与y轴的交点为P,与C的交点为Q,且
与y轴的交点为P,与C的交点为Q,且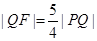 .
.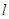 与C相交于A,B两点,若AB的垂直平分线
与C相交于A,B两点,若AB的垂直平分线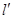 与C相较于M,N两点,且A,M,B,N四点在同一圆上,求
与C相较于M,N两点,且A,M,B,N四点在同一圆上,求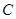 :
: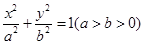 的右焦点为
的右焦点为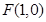 ,短轴的一个端点
,短轴的一个端点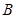 到
到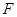 的距离等于焦距.
的距离等于焦距.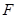 的直线
的直线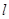 与椭圆
与椭圆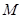 ,
,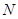 ,是否存在直线
,是否存在直线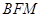 与△
与△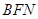 的面积比值为
的面积比值为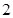 ?若存在,求出直线
?若存在,求出直线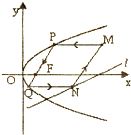
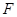 为抛物线
为抛物线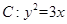 的焦点,过
的焦点,过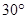 的直线交
的直线交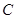 于
于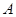 ,
,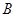 两点,则
两点,则 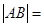 ( )
( )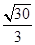
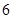
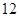
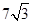
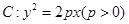 的焦点
的焦点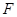 到准线的距离为
到准线的距离为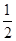 .过点
.过点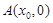
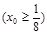
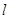 交抛物线
交抛物线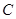 与
与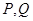 两点(
两点(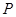 在第一象限内).
在第一象限内).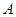 与焦点
与焦点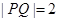 .求直线
.求直线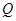 关于
关于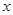 轴的对称点为
轴的对称点为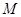 .直线
.直线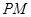 交
交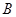 . 且
. 且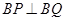 .求点
.求点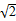 的圆C与直线y=x相切于坐标原点O,椭圆
的圆C与直线y=x相切于坐标原点O,椭圆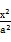 +
+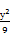 =1与圆C的一个交点到椭圆两焦点的距离之和为10.
=1与圆C的一个交点到椭圆两焦点的距离之和为10.