Question

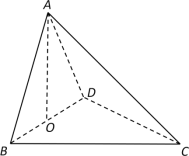
【题目】如图，将边长为2，有一个锐角为60°的菱形ABCD，沿着较短的对角线BD对折，使得，O为BD的中点.

（Ⅰ）求证：

（Ⅱ）求三棱锥的体积；

（Ⅲ）求二面角A-BC-D的余弦值.

Answer 1

【答案】（1）见解析（2）1（3）

【解析】

（Ⅰ）根据为等边三角形可以得到，再根据已知的面面垂直可以得到平面.

（Ⅱ）由（Ⅰ）可以得到到平面的距离为，故可计算也就是.

（Ⅲ）过作交于，连接，则就是所求二面角的平面角，通过解三角形可以得到二面角的余弦值.

（Ⅰ）证明：因为，平面平面，平面，平面平面，所以平面.

（Ⅱ） .

（Ⅲ）过作于，连接，因为平面，所以为在平面上的射影，故， 所以为二面角的平面角.

在 中，，所以，所以 ， 即二面角的余弦值为.