题目内容
一个五位数 满足
满足 且
且 (如37201,45412),则称这个五位数符合“正弦规律”.那么,共有
个五位数符合“正弦规律”.
(如37201,45412),则称这个五位数符合“正弦规律”.那么,共有
个五位数符合“正弦规律”.
【答案】
2892
【解析】
试题分析:首先对五位数 进行分析,可知它的特征是
进行分析,可知它的特征是 是五个数字中最大的一个,
是五个数字中最大的一个, 是一个数字中最小的一个,
是一个数字中最小的一个, 三个有大小不定但都与
三个有大小不定但都与 不相等,因此这个五位数中至少会出现3个不同数字,当做也可能有4个不同数字或者5个不同数字.下面我们就可以根据这三种情形分类讨论,五位数中只有3个不同数字:
不相等,因此这个五位数中至少会出现3个不同数字,当做也可能有4个不同数字或者5个不同数字.下面我们就可以根据这三种情形分类讨论,五位数中只有3个不同数字: ,五位数中只有4个不同数字:
,五位数中只有4个不同数字: ,五位数中只有5个不同数字:
,五位数中只有5个不同数字: ,共有
,共有 个数.
个数.
考点:排列与组合.

练习册系列答案
相关题目
一个五位的自然数
称为“凸”数,当且仅当它满足a<b<c,c>d>e(如12430,13531等),则在所有的五位数中“凸”数的个数是( )
. |
| abcde |
| A、8568 | B、2142 |
| C、2139 | D、1134 |
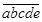 满足
满足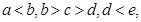 且
且 (如37201,45412),则称这个五位数符合“正弦规律”.那么,共有
个五位数符合“正弦规律”.
(如37201,45412),则称这个五位数符合“正弦规律”.那么,共有
个五位数符合“正弦规律”.