题目内容
已知函数f(x)=sin sin
sin
(1)求函数f(x)在[-π,0]上的单调区间.
(2)已知角α满足α∈ =1,求f(α)的值.
=1,求f(α)的值.
解:f(x)=sin sin
sin
=sin cos
cos =
= sin x.
sin x.
(1)函数f(x)的单调递减区间为 ,单调递增区间为
,单调递增区间为 .
.
(2)2f(2α)+4f =1⇒sin 2α+2sin
=1⇒sin 2α+2sin =1
=1
⇒2sin αcos α+2(cos2α-sin2α)=1
⇒cos2α+2sin αcos α-3sin2α=0
⇒(cos α+3sin α)(cos α-sin α)=0.
∵α∈ ,∴cos α-sin α=0⇒tan α=1得α=
,∴cos α-sin α=0⇒tan α=1得α= ,故sin α=
,故sin α= ,∴f(α)=
,∴f(α)= sin α=
sin α= .
.

练习册系列答案
相关题目
 上的最小值是-2,则ω的最小值等于( )
上的最小值是-2,则ω的最小值等于( ) B.
B.
 的部分图像如图所示.
的部分图像如图所示.
 时,求f(x)的取值范围.
时,求f(x)的取值范围.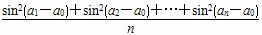 为集合{a1,a2,…,an}相对a0的“正弦方差”,则集合
为集合{a1,a2,…,an}相对a0的“正弦方差”,则集合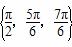 相对a0的“正弦方差”为( )
相对a0的“正弦方差”为( )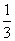
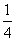 D.与a0有关的一个值
D.与a0有关的一个值 B.
B.  C.
C.  D.
D. 

 ,把函数
,把函数 的零点按从小到大的顺序排列成一个数列,则该数列的通项公式为 ( )
的零点按从小到大的顺序排列成一个数列,则该数列的通项公式为 ( )  B.
B.
 D.
D.
 的值是( )
的值是( )
 是
是 的切线,则
的切线,则 的值为( )
的值为( ) B.
B. C.
C. D.
D.