题目内容
已知函数f(x)=mx3-3(m+1)x2+(3m+6)x+1其中m<0(1)若f(x)的单调增区间是(0,1),求m的值;
(2)当x∈[-1,1]时,函数y=f(x)的图象上任意一点的切线斜率恒大于3m,求m的取值范围.
【答案】分析:(1)已知函数f(x)=mx3-3(m+1)x2+(3m+6)x+1其中m<0,对其进行求导,因为f(x)的单调增区间是(0,1),说明f′(x)≥0,在(0,1)上恒成立,从而求出m的值;
(2)设M(x,y)为y=f(x)(-1≤x≤1)图象上任意一点,切线斜率K=f′(x)=3m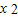 -6(m+1)x+(3m+6)>3m,将问题转化为3m
-6(m+1)x+(3m+6)>3m,将问题转化为3m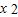 -6(m+1)x+6>0在x∈[-1,1],m<0)则(g(x))min>0,再利用导数研究函数的最值问题,求m的取值范围.
-6(m+1)x+6>0在x∈[-1,1],m<0)则(g(x))min>0,再利用导数研究函数的最值问题,求m的取值范围.
解答:解:(1)f(x)=mx3-3(m+1)x2+(3m+6)x+1,m<0,
f′(x)=mx2-6(m+1)x+(3m+6)(m<0)
因为f(x)的增区间是(0,1)
则f′(x)=3mx2-6(m+1)x+(3m+6)>0的解集为(0,1)
所以f′(0)=3m+6=0,f′(1)=3m-6(m+1)+3m+6=0
解得m=-2 (4分)
(2)设M(x,y)为y=f(x)(-1≤x≤1)图象上任意一点
切线斜率K=f′(x)=3m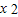 -6(m+1)x+(3m+6)>3m,
-6(m+1)x+(3m+6)>3m,
即3m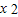 -6(m+1)x+6>0在x∈[-1,1],m<0)则(g(x))min>0,
-6(m+1)x+6>0在x∈[-1,1],m<0)则(g(x))min>0,
g(x)=3m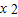 -6(m+1)x+6的对称轴为x=
-6(m+1)x+6的对称轴为x=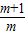 =1+
=1+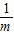 <1
<1
①当1+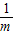 ≤0即-1≤m<0时,(g(x))min=g(1)=-3m>0,∴-1≤m<0;
≤0即-1≤m<0时,(g(x))min=g(1)=-3m>0,∴-1≤m<0;
②当0<1+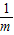 <1即m<-1时,(g(x))min=g(-1)=9m+12>0,此时无解,
<1即m<-1时,(g(x))min=g(-1)=9m+12>0,此时无解,
综上所述:m的取值范围:(-1,0);
点评:此题主要利用导数研究函数的单调性及其最值问题,第二问用到了转化的思想,这是一道综合性比较强的题,为一道中档题;
(2)设M(x,y)为y=f(x)(-1≤x≤1)图象上任意一点,切线斜率K=f′(x)=3m
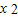 -6(m+1)x+(3m+6)>3m,将问题转化为3m
-6(m+1)x+(3m+6)>3m,将问题转化为3m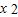 -6(m+1)x+6>0在x∈[-1,1],m<0)则(g(x))min>0,再利用导数研究函数的最值问题,求m的取值范围.
-6(m+1)x+6>0在x∈[-1,1],m<0)则(g(x))min>0,再利用导数研究函数的最值问题,求m的取值范围.解答:解:(1)f(x)=mx3-3(m+1)x2+(3m+6)x+1,m<0,
f′(x)=mx2-6(m+1)x+(3m+6)(m<0)
因为f(x)的增区间是(0,1)
则f′(x)=3mx2-6(m+1)x+(3m+6)>0的解集为(0,1)
所以f′(0)=3m+6=0,f′(1)=3m-6(m+1)+3m+6=0
解得m=-2 (4分)
(2)设M(x,y)为y=f(x)(-1≤x≤1)图象上任意一点
切线斜率K=f′(x)=3m
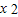 -6(m+1)x+(3m+6)>3m,
-6(m+1)x+(3m+6)>3m,即3m
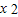 -6(m+1)x+6>0在x∈[-1,1],m<0)则(g(x))min>0,
-6(m+1)x+6>0在x∈[-1,1],m<0)则(g(x))min>0,g(x)=3m
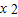 -6(m+1)x+6的对称轴为x=
-6(m+1)x+6的对称轴为x=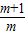 =1+
=1+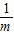 <1
<1①当1+
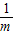 ≤0即-1≤m<0时,(g(x))min=g(1)=-3m>0,∴-1≤m<0;
≤0即-1≤m<0时,(g(x))min=g(1)=-3m>0,∴-1≤m<0;②当0<1+
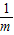 <1即m<-1时,(g(x))min=g(-1)=9m+12>0,此时无解,
<1即m<-1时,(g(x))min=g(-1)=9m+12>0,此时无解,综上所述:m的取值范围:(-1,0);
点评:此题主要利用导数研究函数的单调性及其最值问题,第二问用到了转化的思想,这是一道综合性比较强的题,为一道中档题;

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目