题目内容
【题目】已知圆![]() 的圆心为
的圆心为![]() ,
,![]() 为圆上任意一点,
为圆上任意一点,![]() ,线段
,线段![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() .
.
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)记点![]() 的轨迹为曲线
的轨迹为曲线![]() ,点
,点![]() ,
,![]() .若点
.若点![]() 为直线
为直线![]() 上一动点,且
上一动点,且![]() 不在
不在![]() 轴上,直线
轴上,直线![]() 、
、![]() 分别交曲线
分别交曲线![]() 于
于![]() 、
、![]() 两点,求四边形
两点,求四边形![]() 面积的最大值.
面积的最大值.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)线段![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() ,则
,则![]() .所以
.所以![]() ,即点
,即点![]() 在以
在以![]() 、
、![]() 为焦点,长轴长为4的椭圆上,即可求出轨迹方程.
为焦点,长轴长为4的椭圆上,即可求出轨迹方程.
(2)设![]() ,由于椭圆关于
,由于椭圆关于![]() 轴对称,所以不妨设
轴对称,所以不妨设![]() 则直线
则直线![]() 的方程为:
的方程为:![]() ,直线
,直线![]() 的方程为:
的方程为:![]() .设
.设![]() ,
,![]() ,联立直线方程与椭圆方程,即可求出
,联立直线方程与椭圆方程,即可求出![]() ,
,![]() 的坐标,而
的坐标,而![]()
再用基本不等式的性质及函数的性质求出面积最值.
解:(1)由题意,线段![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() ,则
,则![]() .
.
所以![]() ,
,
即点![]() 在以
在以![]() 、
、![]() 为焦点,长轴长为4的椭圆上,
为焦点,长轴长为4的椭圆上,
所以![]() ,
,![]() ,
,![]()
故点![]() 的轨迹方程为:
的轨迹方程为:![]() ;
;
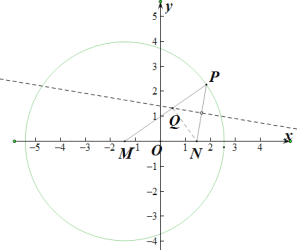
(2)设![]() ,由于椭圆关于
,由于椭圆关于![]() 轴对称,所以不妨设
轴对称,所以不妨设![]()
则直线![]() 的方程为:
的方程为:![]() ,直线
,直线![]() 的方程为:
的方程为:![]() .
.
设![]() ,
,![]()
由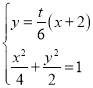 得
得![]() ,则
,则![]() ,
,
即![]() ,于是
,于是![]() .
.
同理可得:![]() ,
,![]()
所以![]()
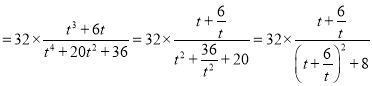
设![]() ,则
,则![]() ,则
,则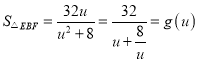
![]() 在
在![]() 单调递减,故
单调递减,故![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某鲜花店每天制作![]() 、
、![]() 两种鲜花共
两种鲜花共![]() 束,每束鲜花的成本为
束,每束鲜花的成本为![]() 元,售价
元,售价![]() 元,如果当天卖不完,剩下的鲜花作废品处理.该鲜花店发现这两种鲜花每天都有剩余,为此整理了过往100天这两种鲜花的日销量(单位:束),得到如下统计数据:
元,如果当天卖不完,剩下的鲜花作废品处理.该鲜花店发现这两种鲜花每天都有剩余,为此整理了过往100天这两种鲜花的日销量(单位:束),得到如下统计数据:
| 48 | 49 | 50 | 51 |
天数 | 25 | 35 | 20 | 20 |
| 48 | 49 | 50 | 51 |
天数 | 40 | 35 | 15 | 10 |
以这100天记录的各销量的频率作为各销量的概率,假设这两种鲜花的日销量相互独立.
(1)记该店这两种鲜花每日的总销量为![]() 束,求
束,求![]() 的分布列.
的分布列.
(2)鲜花店为了减少浪费,提升利润,决定调查每天制作鲜花的量![]() 束.以销售这两种鲜花的日总利润的期望值为决策依据,在每天所制鲜花能全部卖完与
束.以销售这两种鲜花的日总利润的期望值为决策依据,在每天所制鲜花能全部卖完与![]() 之中选其一,应选哪个?
之中选其一,应选哪个?