题目内容
已知在函数f(x)=mx3-x的图象上以点N(1,n)为切点的切线的倾斜角为
.
(Ⅰ)求m,n的值;
(Ⅱ)是否存在最小的正整数k,使得不等式f(x)≤k-1992对于x∈[-1,3]恒成 立?如果存在,请求出最小的正整数k,如果不存在,请说明理由.
| π | 4 |
(Ⅰ)求m,n的值;
(Ⅱ)是否存在最小的正整数k,使得不等式f(x)≤k-1992对于x∈[-1,3]恒成 立?如果存在,请求出最小的正整数k,如果不存在,请说明理由.
分析:(Ⅰ)根据导数的几何意义求出函数f(x)在x=1处的导数,得到切线的斜率等于tan
.建立等式关系,求出m的值,再将切点代入曲线方程,求出n的值;
(Ⅱ)要使得不等式f(x)≤k-1992对于x∈[-1,3]恒成立,即求k≥[1992+f(x)]max,先求出f′(x)=0的值,再讨论满足f′(x)=0的点附近的导数的符号的变化情况,来确定极值,将f(x)的各极值与其端点的函数值比较,其中最大的一个就是最大值,即可求出k的最小值.
| π |
| 4 |
(Ⅱ)要使得不等式f(x)≤k-1992对于x∈[-1,3]恒成立,即求k≥[1992+f(x)]max,先求出f′(x)=0的值,再讨论满足f′(x)=0的点附近的导数的符号的变化情况,来确定极值,将f(x)的各极值与其端点的函数值比较,其中最大的一个就是最大值,即可求出k的最小值.
解答:解:(Ⅰ)f′(x)=3mx2-1,f′(1)=1,∴3m-1=1,∴m=
.
∴f(x)=
x3-x,f(1)=
-1=-
.
又点N(1,n)在曲线上,∴n=-
.…(6分)
(Ⅱ)由f′(x)=2x2-1,x∈[-1,3]知,
当x∈(-1, -
)∪(
,3)时f′(x)>0;
当x∈(-
,
)时f′(x)<0,
∴f(x)在[-1,-
]和[
,3]上递增,在[-
,
]上递减.…(8分)
∵f(-
)=
,f(3)=15,∴f(x)在[-1,3]上最大值为15.∴k-1992≥15,k≥2007.
故存在最小自然数2007.…(12分)
| 2 |
| 3 |
∴f(x)=
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
又点N(1,n)在曲线上,∴n=-
| 1 |
| 3 |
(Ⅱ)由f′(x)=2x2-1,x∈[-1,3]知,
当x∈(-1, -
| ||
| 2 |
| ||
| 2 |
当x∈(-
| ||
| 2 |
| ||
| 2 |
∴f(x)在[-1,-
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
∵f(-
| ||
| 2 |
| ||
| 3 |
故存在最小自然数2007.…(12分)
点评:本题以三次函数的切线为载体,主要考查了利用导数研究曲线上某点切线方程,以及函数恒成立问题等基础题知识,考查运算求解能力,属于中档题.

练习册系列答案
相关题目
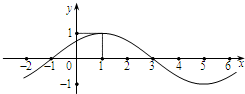 已知函数f(x)=Asin(ωx+φ)(其中x∈R,A>0,ω>0,
已知函数f(x)=Asin(ωx+φ)(其中x∈R,A>0,ω>0, (2012•东城区二模)已知函数f(x)=Asin(ωx+φ)(其中x∈R,A>0,ω>0,-
(2012•东城区二模)已知函数f(x)=Asin(ωx+φ)(其中x∈R,A>0,ω>0,-