Question

（2012•东城区二模）已知函数f（x）=Asin（ωx+φ）（其中x∈R，A＞0，ω＞0，-

π

2

＜φ＜

π

2

）的部分图象如图所示．
（Ⅰ）求函数f（x）的解析式；
（Ⅱ）已知在函数f（x）的图象上的三点M，N，P的横坐标分别为-1，1，5，求sin∠MNP的值．

Answer 1

分析：（Ⅰ）利用最高点确定A的值，利用周期，确定ω的值，利用最高点的坐标，确定φ的值，即可求函数f（x）的解析式；
（Ⅱ）确定点M，N，P的坐标，再利用余弦定理，即可求sin∠MNP的值．

解答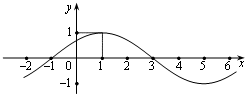：解：（Ⅰ）由图可知，A=1，最小正周期T=4×2=8．
由T=

2π

ω

=8，得ω=

π

4

．…（3分）
又f（1）=sin（

π

4

+φ）=1，且-

π

2

＜φ＜

π

2

，
所以

π

4

+φ=

π

2

，即φ=

π

4

．…（5分）
所以f（x）=sin（

π

4

x+

π

4

）．…（6分）
（Ⅱ）因为f（-1）=0，f（1）=1，f（5）=-1
所以M（-1，0），N（1，1），P（5，-1）．…（7分）
所以|MN|=

5

，|PN|=

20

，|MP|=

37

．
由余弦定理得cos∠MNP=

5+20-37

2 5 × 20

=-

3

5

．           …（11分）
因为∠MNP∈[0，π），所以sin∠MNP=

4

5

．…（13分）

点评：本题考查三角函数模型的建立，考查余弦定理的运用，考查数形结合的数学思想，考查学生分析解决问题的能力，属于中档题．