题目内容
如图,已知⊙O的半径为1,MN是⊙O的直径,过M点作⊙O的切线AM,C是AM的中点,AN交⊙O于B点,若四边形BCON是平行四边形.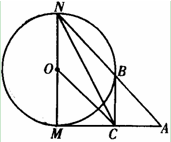
(Ⅰ)求AM的长;
(Ⅱ)求sin∠ANC.
(1)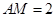 ;(2)
;(2)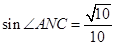 .
.
解析试题分析:本题主要以圆为几何背景考查切线的性质以及求边长求角,可以运用平行四边形的知识证平行和相等.第一问,由于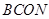 是平行四边形,所以
是平行四边形,所以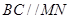 ,因为
,因为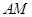 是圆
是圆 的切线,所以
的切线,所以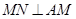 ,所以
,所以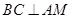 ,又因为
,又因为 是
是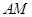 的中点,所以
的中点,所以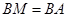 ,所以符合等腰三角形的性质;第二问,在
,所以符合等腰三角形的性质;第二问,在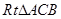 中先求
中先求 ,在
,在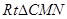 中,求
中,求 ,在
,在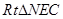 中,求
中,求 .
.
试题解析:(Ⅰ)连接 ,则
,则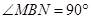 ,因为四边形
,因为四边形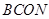 是平行四边形,所以
是平行四边形,所以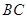 ∥
∥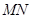 ,因为
,因为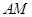 是
是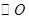 的切线,所以
的切线,所以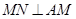 ,可得
,可得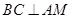 ,又因为
,又因为 是
是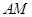 的中点,所以
的中点,所以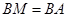 ,得
,得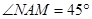 ,故
,故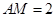 . (5分)
. (5分)
(Ⅱ)作 于
于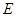 点,则
点,则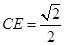 ,由(Ⅰ)可知
,由(Ⅰ)可知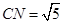 ,
,
故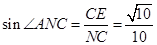 . (10分)
. (10分)
考点:1.切线的性质;2.直角三角形的性质;3.求正弦函数的函数值.

练习册系列答案
相关题目

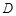 为锐角
为锐角 的内切圆圆心,过点
的内切圆圆心,过点 作直线
作直线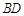 的垂线,垂足为
的垂线,垂足为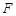 ,圆
,圆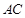 相切于点
相切于点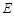 .若
.若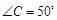 ,求
,求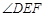 的度数.
的度数.
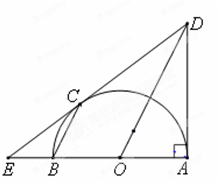
 是以线段
是以线段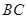 为直径的圆
为直径的圆 上一点,
上一点,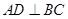 于点
于点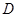 ,过点
,过点 作圆
作圆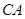 的延长线交于点
的延长线交于点 ,点
,点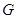 是
是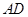 的中点,连结
的中点,连结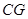 并延长与
并延长与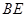 相交于点
相交于点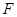 ,延长
,延长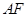 与
与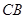 的延长线相交于点
的延长线相交于点 .
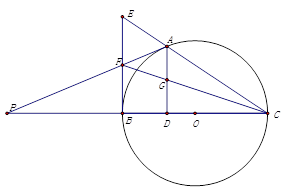
.
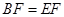 ;
;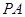 是圆
是圆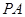 与圆
与圆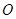 相切于点
相切于点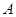 ,直径
,直径 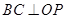 ,连结
,连结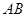 交
交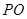 于点
于点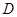 .
.
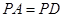 ;
;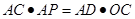 .
.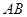 为圆的切线,切点为
为圆的切线,切点为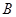 ,点
,点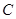 在圆上,
在圆上, 的角平分线
的角平分线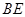 交圆于点
交圆于点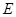 ,
,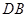 垂直
垂直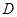 。
。
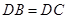 ;
; ,
,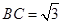 ,延长
,延长 交
交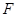 ,求
,求 外接圆的半径。
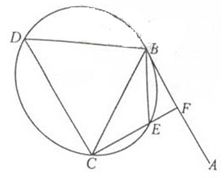
外接圆的半径。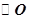 的直径,D为
的直径,D为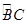 的中点,E为BC的中点.
的中点,E为BC的中点.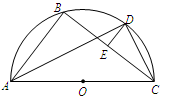
 为直角三角形,
为直角三角形,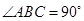 ,以
,以 为直径的圆交
为直径的圆交 于点
于点 ,点
,点 是
是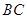 边的中点,连
边的中点,连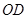 交圆
交圆 于点
于点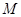 .
.
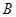 、
、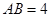 ,
,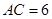 ,求
,求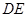 的长.
的长.