题目内容
已知函数 ,其中
,其中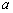 为常数.
为常数.
(Ⅰ)若函数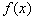 是区间
是区间 上的增函数,求实数
上的增函数,求实数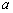 的取值范围;
的取值范围;
(Ⅱ)若 在
在 时恒成立,求实数
时恒成立,求实数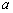 的取值范围.
的取值范围.
解:(Ⅰ) ,
, . -
. -
因为函数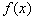 是区间
是区间 上的增函数,
上的增函数,
所以 ,即
,即 在
在 上恒成立.-
上恒成立.-
因为 是增函数,
是增函数,
所以满足题意只需 ,即
,即 . --
. --
(Ⅱ)令 ,解得
,解得 -
-
 的情况如下:
的情况如下:
|
|
|
|
|
|
|
| 0 |
|
|
| ↘ | 极小值 | ↗ |
①当 ,即
,即 时,
时,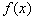 在
在 上的最小值为
上的最小值为 ,
,
若满足题意只需 ,解得
,解得 ,
,
所以此时, ;
;
②当 ,即
,即 时,
时,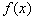 在
在 上的最小值为
上的最小值为 ,
,
若满足题意只需 ,求解可得此不等式无解,
,求解可得此不等式无解,
所以 不存在;
不存在;
③当 ,即
,即 时,
时,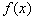 在
在 上的最小值为
上的最小值为 ,
,
若满足题意只需 ,解得
,解得 ,
,
所以此时, 不存在. -分
不存在. -分
综上讨论,所求实数 的取值范围为
的取值范围为 .
.

练习册系列答案
相关题目
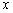






 是抛物线
是抛物线
 上一点,经过点
上一点,经过点 的直线
的直线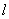 与抛物
与抛物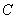 交于
交于 两点.
两点. (I)求证:
(I)求证: 为定值;
为定值; 的面积为
的面积为 ,求直线
,求直线 ,己知
,己知 ,且满足
,且满足 ,则该医院30天内因患H1N1流感就诊的人数共有 .
,则该医院30天内因患H1N1流感就诊的人数共有 . 若关于
若关于 有三个不等的实根,则实数
有三个不等的实根,则实数 的取值范围是
的取值范围是 B.
B.  C.
C.  D.
D. 

 B.
B. 
 D.
D. 
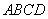 中有一个不规则的图形
中有一个不规则的图形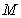 ,用随机模拟方法来估计不规则图形的面积.若在正方形
,用随机模拟方法来估计不规则图形的面积.若在正方形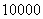 个点,落在不规则图形
个点,落在不规则图形 的图象为曲线
的图象为曲线 ,函数
,函数 的图象为曲线
的图象为曲线 ,过
,过 轴上的动点
轴上的动点 作垂直于
作垂直于 两点,则线段
两点,则线段 长度的最大值为
长度的最大值为 
 中,角
中,角 所对的边分别为
所对的边分别为 ,且
,且

 .
. 的最大值;
的最大值; ,求b的值.
,求b的值.