题目内容
7.已知sin36°=cos54°,可求得cos2016°的值为-$\frac{\sqrt{5}+1}{4}$..分析 利用诱导公式即可化简求值.
解答 解:∵sin36°=cos54°
⇒2sin18°cos18°=cos(18°+18°+18°)
⇒2sin18°cos18°=cos(18°+18°)cos18°-sin(18°+18°)sin18°
⇒2sin18°cos18°=(2cos218°-1)cos18°-2sin218°cos18°
⇒2sin18°cos18°=2cos318°-cos18°-2sin218°cos18°
⇒2sin18°=2cos218°-1-2sin218°
⇒4sin218°+2sin18°-1=0
⇒sin18°=$\frac{-2+\sqrt{{2}^{2}+16}}{2×4}$=$\frac{\sqrt{5}-1}{4}$,
∴cos2016°=cos(360°×5+180°+36°)=-cos36°=2sin218°-1=-$\frac{\sqrt{5}+1}{4}$.
故答案为:-$\frac{\sqrt{5}+1}{4}$.
点评 本题主要考查了诱导公式的应用,考查了概念的理解和运算能力,属于中档题.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
17.已知函数f(x)=$\sqrt{{x}^{2}-2x-3}$,则该函数的单调递增区间为( )
| A. | (-∞,1] | B. | [3,+∞) | C. | (-∞,-1] | D. | [1,+∞) |
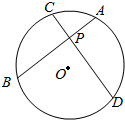 如图,某工业园区是半径为10km的圆形区域,距离园区中心O点5km处有一中转站P,现准备在园区内修建一条笔直公路AB经过中转站,公路AB把园区分成两个区域.
如图,某工业园区是半径为10km的圆形区域,距离园区中心O点5km处有一中转站P,现准备在园区内修建一条笔直公路AB经过中转站,公路AB把园区分成两个区域.