题目内容
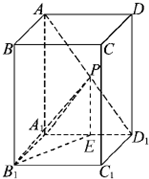 如图所示,已知ABCD-A1B1C1D1是底面为正方形的长方体,∠AD1A1=60°,AD1=4,点P是AD1上的动点.
如图所示,已知ABCD-A1B1C1D1是底面为正方形的长方体,∠AD1A1=60°,AD1=4,点P是AD1上的动点.(1)当P为AD1的中点时,求异面直线AA1与B1P所成角的余弦值;
(2)求PB1与平面AA1D1所成角的正切值的最大值.
分析:(1)解法一:过点P作PE⊥A1D1,垂足为E,连接B1E,则PE∥AA1,可得∠B1PE是异面直线AA1与B1P所成的角,在Rt△B1PE中,利用余弦函数可求异面异面直线AA1与B1P所成角的余弦值;
解法二:以A1为原点,A1B1所在的直线为x轴建立空间直角坐标系,利用坐标表示点与向量,利用向量的夹角公式,即可求得结论;
(2)由(1)知,B1A1⊥平面AA1D1,故∠B1PA1是PB1与平面AA1D1所成的角且tan∠B1PA1=
=
,当A1P最小时,tan∠B1PA1最大,由此可得结论.
解法二:以A1为原点,A1B1所在的直线为x轴建立空间直角坐标系,利用坐标表示点与向量,利用向量的夹角公式,即可求得结论;
(2)由(1)知,B1A1⊥平面AA1D1,故∠B1PA1是PB1与平面AA1D1所成的角且tan∠B1PA1=
| B1A1 |
| A1P |
| 2 |
| A1P |
解答:(1)解法一:过点P作PE⊥A1D1,垂足为E,连接B1E(如图),则PE∥AA1,
∴∠B1PE是异面直线AA1与B1P所成的角.
在Rt△AA1D中,∵∠AD1A1=60°,∴∠A1AD1=30°,

∴A1B1=A1D1=
AD1=2,A1E=
A1D1=1.
又PE=
AA1=
.
∴在Rt△B1PE中,B1P=
=2
,
cos∠B1PE=
=
=
.
∴异面异面直线AA1与B1P所成角的余弦值为
.
解法二:以A1为原点,A1B1所在的直线为x轴建立空间直角坐标系如图所示,则A1(0,0,0),A(0,0,2
),B1(2,0,0),P(0,1,
),∴
=(0,0,2
),
=(-2,1,
),
∴cos<
,
>=
=
∴异面直线AA1与B1P所成角的余弦值为
.
(2)由(1)知,B1A1⊥平面AA1D1,
∴∠B1PA1是PB1与平面AA1D1所成的角且tan∠B1PA1=
=
,
当A1P最小时,tan∠B1PA1最大,这时A1P⊥AD1,由A1P=
=
,得tan∠B1PA1=
,
即PB1与平面AA1D1所成角的正切值的最大值为
.
∴∠B1PE是异面直线AA1与B1P所成的角.
在Rt△AA1D中,∵∠AD1A1=60°,∴∠A1AD1=30°,

∴A1B1=A1D1=
| 1 |
| 2 |
| 1 |
| 2 |
又PE=
| 1 |
| 2 |
| 3 |
∴在Rt△B1PE中,B1P=
| 5+3 |
| 2 |
cos∠B1PE=
| PE |
| B1P |
| ||
2
|
| ||
| 4 |
∴异面异面直线AA1与B1P所成角的余弦值为
| ||
| 4 |
解法二:以A1为原点,A1B1所在的直线为x轴建立空间直角坐标系如图所示,则A1(0,0,0),A(0,0,2
| 3 |
| 3 |
| A1A |
| 3 |
| B1P |
| 3 |
∴cos<
| A1A |
| B1P |
| ||||
|
|
| ||
| 4 |
∴异面直线AA1与B1P所成角的余弦值为
| ||
| 4 |
(2)由(1)知,B1A1⊥平面AA1D1,
∴∠B1PA1是PB1与平面AA1D1所成的角且tan∠B1PA1=
| B1A1 |
| A1P |
| 2 |
| A1P |
当A1P最小时,tan∠B1PA1最大,这时A1P⊥AD1,由A1P=
| A1D1•A1A |
| AD1 |
| 3 |
2
| ||
| 3 |
即PB1与平面AA1D1所成角的正切值的最大值为
2
| ||
| 3 |
点评:本题考查线线角,考查线面角,解题的关键是正确作出线线角与线面角,属于中档题.

练习册系列答案
相关题目
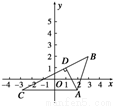
 如图所示,已知△ABC在第一象限,若A(1,1),B(5,1),A=60°,B=45°,求:
如图所示,已知△ABC在第一象限,若A(1,1),B(5,1),A=60°,B=45°,求: 如图所示,已知△ABC的水平放置的直观图是等腰直角△A′B′C′,∠A′=90°,
如图所示,已知△ABC的水平放置的直观图是等腰直角△A′B′C′,∠A′=90°, (2013•湖南模拟)如图所示,已知△ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,DC⊥平面ABC,AB=2,tan∠EAB=
(2013•湖南模拟)如图所示,已知△ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,DC⊥平面ABC,AB=2,tan∠EAB= 如图所示,已知△ABC中,AD是BC边上的中线,E是AD的中点,BE的延长线交AC于点F,则AF:AC=
如图所示,已知△ABC中,AD是BC边上的中线,E是AD的中点,BE的延长线交AC于点F,则AF:AC= 及点D的坐标.
及点D的坐标.