题目内容
【题目】设![]() 是公差不为零的等差数列,满足
是公差不为零的等差数列,满足![]() ,
,![]() ,设正项数列
,设正项数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() .
.
(1)求数列![]() 和
和![]() 的通项公式;
的通项公式;
(2)在![]() 和
和![]() 之间插入1个数
之间插入1个数![]() ,使
,使![]() 、
、![]() 、
、![]() 成等差数列;在
成等差数列;在![]() 和
和![]() 之间插入2个数
之间插入2个数![]() 、
、![]() ,使
,使![]() 、
、![]() 、
、![]() 、
、![]() 成等差数列;
成等差数列;![]() ;在
;在![]() 和
和![]() 之间插入
之间插入![]() 个数
个数![]() 、
、![]() 、
、![]() 、
、![]() ,使
,使![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 成等差数列.
成等差数列.
① 求![]() ;
;
② 对于①中的![]() ,是否存在正整数
,是否存在正整数![]() 、
、![]() ,使得
,使得![]() 成立?若存在,求出所有的正整数对
成立?若存在,求出所有的正整数对![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
【答案】(1)![]() ,
,![]() ;(2)①
;(2)①![]() ;②存在符合题意的正整数对
;②存在符合题意的正整数对![]() ,它们为
,它们为![]() 和
和![]() .
.
【解析】
(1)求出等差数列的首项和公差即得数列![]() 的通项公式,由题得当
的通项公式,由题得当![]() 时,
时,![]() ,
,![]() ,相减即得
,相减即得![]() 的通项公式;
的通项公式;
(2)①![]() ,再利用错位相减法求和得解;②假设存在正整数
,再利用错位相减法求和得解;②假设存在正整数![]() ,使得
,使得![]() ,化简得
,化简得![]() ,令
,令![]() ,证明
,证明![]() 时,
时,![]() ,列举得解.
,列举得解.
(1)设数列![]() 的公差为
的公差为![]() ,则由
,则由![]() 可得
可得![]() ,
,
再由![]() 化简得:
化简得:![]() ,解得:
,解得:![]() ,∴
,∴![]() ,
,
当![]() 时,
时,![]() 得:
得:![]() ;当
;当![]() 时,
时,![]() ,
,![]() ,
,
两式相减得![]() ,∴
,∴![]() .
.
(2)①![]() ,
,
![]() ,
,
设![]() ,
,
所以![]() ,
,
上面两式错位相减得![]() ,
,
所以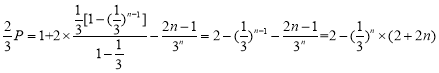
所以![]() ,
,
∴![]() .
.
②假设存在正整数![]() ,使得
,使得![]() ,
,
代入化简得![]() ,即
,即![]() ,
,
令![]() ,
,
则由![]() 可得:
可得:![]() .
.
当![]() 时,
时,![]() ,
,
∴![]() ,即
,即![]() ,舍去;
,舍去;
当![]() 时,
时,![]() ,舍去;
,舍去;
当![]() 时,
时,![]() ,符合题意;
,符合题意;
当![]() 时,
时,![]() ,符合题意;
,符合题意;
综上:存在符合题意的正整数对![]() ,它们为
,它们为![]() 和
和![]() .
.

 金钥匙试卷系列答案
金钥匙试卷系列答案【题目】某公司为提高市场销售业绩,促进某产品的销售,随机调查了该产品的月销售单价![]() (单位:元/件)及相应月销量
(单位:元/件)及相应月销量![]() (单位:万件),对近5个月的月销售单价
(单位:万件),对近5个月的月销售单价![]() 和月销售量
和月销售量![]() 的数据进行了统计,得到如下表数据:
的数据进行了统计,得到如下表数据:
月销售单价 | 9 |
| 10 |
| 11 |
月销售量 | 11 | 10 | 8 | 6 | 5 |
(Ⅰ)建立![]() 关于
关于![]() 的回归直线方程;
的回归直线方程;
(Ⅱ)该公司开展促销活动,当该产品月销售单价为7元/件时,其月销售量达到18万件,若由回归直线方程得到的预测数据与此次促销活动的实际数据之差的绝对值不超过![]() 万件,则认为所得到的回归直线方程是理想的,试问:(Ⅰ)中得到的回归直线方程是否理想?
万件,则认为所得到的回归直线方程是理想的,试问:(Ⅰ)中得到的回归直线方程是否理想?
(Ⅲ)根据(Ⅰ)的结果,若该产品成本是5元/件,月销售单价![]() 为何值时(销售单价不超过11元/件),公司月利润的预计值最大?
为何值时(销售单价不超过11元/件),公司月利润的预计值最大?
参考公式:回归直线方程![]() ,其中
,其中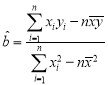 ,
,![]() .
.
参考数据:![]() ,
,![]() .
.