题目内容
在直角坐标平面上的点集 ,
, ,那么
,那么 的面积是
的面积是
A. B.
B. C.
C. D.
D.
【答案】
C
【解析】
试题分析: 表示圆
表示圆 的内部,集合M中
的内部,集合M中 整理为
整理为 或
或 其中当
其中当 时
时 表示直线
表示直线 ,x轴负半轴,圆
,x轴负半轴,圆 围成的图形与直线
围成的图形与直线 ,y轴正半轴,圆
,y轴正半轴,圆 围成的图形,两图形均为扇形,面积和为圆的
围成的图形,两图形均为扇形,面积和为圆的 ,当
,当 时
时 表示的图形是圆
表示的图形是圆 在第四象限的部分,综上可知总面积为圆面积的一半,即
在第四象限的部分,综上可知总面积为圆面积的一半,即
考点:不等式表示平面区域
点评:集合N相对比较简单,集合M中的不等式化简后包括多种情况,如 就又包含了
就又包含了 ,
, 两种情况,分情况讨论题目对学生一直是难点
两种情况,分情况讨论题目对学生一直是难点

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
已知z是实系数方程x2+2bx+c=0的虚根,记它在直角坐标平面上的对应点为Pz,
(1)若(b,c)在直线2x+y=0上,求证:Pz在圆C1:(x-1)2+y2=1上;
(2)给定圆C:(x-m)2+y2=r2(m、r∈R,r>0),则存在唯一的线段s满足:①若Pz在圆C上,则(b,c)在线段s上;②若(b,c)是线段s上一点(非端点),则Pz在圆C上、写出线段s的表达式,并说明理由;
(3)由(2)知线段s与圆C之间确定了一种对应关系,通过这种对应关系的研究,填写表(表中s1是(1)中圆C1的对应线段).
(1)若(b,c)在直线2x+y=0上,求证:Pz在圆C1:(x-1)2+y2=1上;
(2)给定圆C:(x-m)2+y2=r2(m、r∈R,r>0),则存在唯一的线段s满足:①若Pz在圆C上,则(b,c)在线段s上;②若(b,c)是线段s上一点(非端点),则Pz在圆C上、写出线段s的表达式,并说明理由;
(3)由(2)知线段s与圆C之间确定了一种对应关系,通过这种对应关系的研究,填写表(表中s1是(1)中圆C1的对应线段).
| 线段s与线段s1的关系 | m、r的取值或表达式 |
| s所在直线平行于s1所在直线 | |
| s所在直线平分线段s1 |
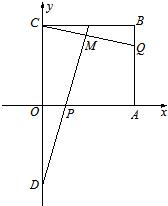 如图所示,在直角坐标平面上的矩形OABC中,|OA|=2,
如图所示,在直角坐标平面上的矩形OABC中,|OA|=2,