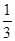题目内容
已知a,b,c都是正数，求证：2(
-
)≤3(
).
思路分析：用分析法去找一找证题的突破口.要证原不等式,只需证-2≤c-3,即只需证c+2≥3
，把2
变化为
+
,问题就解决了.或由分析法的途径,也很容易用综合法的形式写出证明过程.
证法一:要证2(
-
)≤3(
),只需证a+b-2
≤a+b+c-3
,
即-2
≤c-3
.移项,得c+2
≥3
.
由a,b,c为正数,得c+2
=c+
+
≥3
.
∴原不等式成立.
证法二:∵a,b,c是正数,
∴c+
+
≥
.
即c+2
≥3
.故-2
≤c-3
.
∴a+b-2
≤a+b+c-3
,
∴2(
-
)≤3(
).
练习册系列答案
寒假天地重庆出版社系列答案
相关题目
,则( )
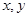都是正实数，求证：
；
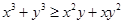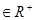,且a+b+c=1, 求证：a2+b2+c2≥
﹥ 