题目内容
（Ⅰ）已知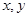
都是正实数，求证：
；
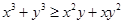（2）已知a,b,c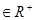
,且a+b+c=1, 求证：a2+b2+c2≥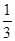
【答案】
Ⅰ）证明：∵
，
又∵
，∴
，∴
，
∴
．…………………５分
（2）证明：由a+b+c=1, 得1=（a+b+c）2= a2+b2+c2+2ab+2bc+2ac≤3（a2+b2+c2）
∴a2+b2+c2≥
．（当且仅当a=b=c时取等号）
【解析】(I)可以利用作差比较然后提取公因式，转化为若干个因式积的形式，再逐一判断积的符号.
（II）对a+b+c=1两边平方，再利用
证明即可.
练习册系列答案
相关题目
都是正实数，求证：
；
都是正数，求证：
.
都是正实数， 函数
的图象过
点，则
的最小值是 .
都是正实数，求证：
；
,且a+b+c=1, 求证：a2+b2+c2≥
都是正实数，求证：
；
都是正数，求证：
.
都是正实数，求证：
；
,且a+b+c=1,求证：a2+b2+c2≥
．