题目内容
1.已知数列{an}中,${a_1}=1,{a_{n+1}}=\frac{a_n}{{{a_n}+2}}(n∈{N^*})$(Ⅰ)求证:$\left\{{\frac{1}{a_n}+1}\right\}$是等比数列,并求{an}的通项公式an;
(Ⅱ)数列{bn}满足${b_n}=({2^n}-1)•\frac{n}{{{2^{n-1}}}}•{a_n}$,数列{bn}的前n项和为Tn,若不等式${(-1)^n}λ<{T_n}+\frac{n}{{{2^{n-1}}}}$对一切n∈N*恒成立,求λ的取值范围.
分析 (Ⅰ)由${a}_{n+1}=\frac{{a}_{n}}{{a}_{n+2}}$,得$\frac{1}{{a}_{n+1}}$+1=2($\frac{1}{{a}_{n}}+1$),由此能证明$\left\{{\frac{1}{a_n}+1}\right\}$是以2为首项,2为公比的等比数列,并能求出{an}的通项公式an.
(Ⅱ)由bn=$\frac{n}{{2}^{n-1}}$,利用错位相减法能求出Tn=4-$\frac{n+2}{{2}^{n-1}}$,从而(-1)nλ<4-$\frac{2}{{2}^{n-1}}$,由此能求出λ的取值范围.
解答 证明:(Ⅰ)由${a}_{n+1}=\frac{{a}_{n}}{{a}_{n+2}}$,得$\frac{1}{{a}_{n+1}}$=$\frac{{a}_{n}+2}{{a}_{n}}$=1+$\frac{2}{{a}_{n}}$,
即$\frac{1}{{a}_{n+1}}$+1=2($\frac{1}{{a}_{n}}+1$),
又$\frac{1}{{a}_{1}}+1=2$,∴$\left\{{\frac{1}{a_n}+1}\right\}$是以2为首项,2为公比的等比数列.
∴$\frac{1}{{a}_{n}}$+1=2×2n-1=2n,即${a}_{n}=\frac{1}{{2}^{n}-1}$.…(6分)
解:(Ⅱ)bn=$\frac{n}{{2}^{n-1}}$,
Tn=1×$\frac{1}{{2}^{0}}+2×\frac{1}{2}+3×\frac{1}{{2}^{2}}$+…+(n-1)×$\frac{1}{{2}^{n-2}}+n×\frac{1}{{2}^{n-1}}$,
$\frac{1}{2}{T}_{n}$=$1×\frac{1}{2}+2×\frac{1}{{2}^{2}}+…+(n-1)×\frac{1}{{2}^{n-1}}+n×\frac{1}{{2}^{n}}$,
两式相减得:
$\frac{1}{2}{T}_{n}$=$\frac{1}{{2}^{0}}+\frac{1}{2}+\frac{1}{{2}^{2}}+…+\frac{1}{{2}^{n-1}}$-n×$\frac{1}{{2}^{n}}$=2-$\frac{n+2}{{2}^{n}}$,
Tn=4-$\frac{n+2}{{2}^{n-1}}$,…(9分)
∴(-1)nλ<4-$\frac{2}{{2}^{n-1}}$,
令Sn=4-$\frac{2}{{2}^{n-1}}$,由题意知Sn单调递增.
若n为偶数,则λ<4-$\frac{2}{{2}^{n-1}}$,Sn|min=S2=3,
∴λ<3.
若n为奇数,则-λ<4-$\frac{2}{{2}^{n-1}}$,Sn|min=S1=2,
∴-λ<2,∴λ>-2,
∴-2<λ<3.即λ的取值范围是(-2,3).
点评 本题考查等比数列的证明,考查数列的通项公式的求法,考查实数的取值范围的求法,是中档题,解题时要注意错位相减法的合理运用.

 名校课堂系列答案
名校课堂系列答案| A. | (0,10) | B. | (-1,2) | C. | (0,1) | D. | (1,10) |
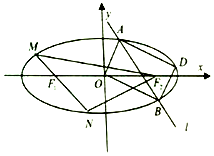 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),短轴长2,两焦点分别为F1,F2,过F1的直线交椭圆C于M,N两点,且△F2MN的周长为8.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),短轴长2,两焦点分别为F1,F2,过F1的直线交椭圆C于M,N两点,且△F2MN的周长为8.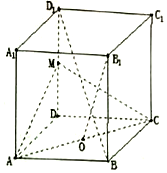 在正方体ABCD-A1B1C1D1中,M为DD1的中点,O为AC的中点,AB=1.
在正方体ABCD-A1B1C1D1中,M为DD1的中点,O为AC的中点,AB=1.