题目内容
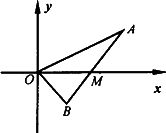
如图,线段AB过x轴正半轴上一点M(m,0)(m>0),端点A、B到x轴距离之积为2m,以x轴为对称轴,过A、O、B三点作抛物线.(1)求抛物线方程;
(2)若m为定值,求△AOB面积的最小值;
(3)若∠AOB=
 ,求实数m的取值范围.
,求实数m的取值范围.
【答案】分析:(1)设直线AB方程为:x=ky+m,抛物线方程为:y2=2px(p>0),由 得,y2-2pky-2pm=0,再由韦达定理能够导出抛物线方程;
得,y2-2pky-2pm=0,再由韦达定理能够导出抛物线方程;
(2)由 =
= ,能够导出△AOB面积的最小值;
,能够导出△AOB面积的最小值;
(3) =
=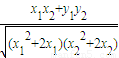 =
=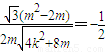 ,由此能求出实数m的取值范围.
,由此能求出实数m的取值范围.
解答:解:(1)设直线AB方程为:x=ky+m,抛物线方程为:y2=2px(p>0),
由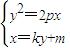 得,y2-2pky-2pm=0,
得,y2-2pky-2pm=0,
设A(x1,y1),B(x2,y2),则有 ,
,
由题意,|-2pm|=2m⇒2p=2,
故所求抛物线方程为:y2=2x;
(2)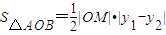
=
 =m
=m .
.
(3)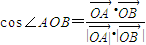 =
=
=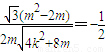 ,
,
∴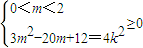 ,
,
∴ .
.
点评:本题考查抛物线方程的求法,求△AOB面积的最小值和求实数m的取值范围.解题时要认真审题,仔细挖掘题设中的隐含条件,灵活运用抛物线的性质,合理地进行等价转化.
 得,y2-2pky-2pm=0,再由韦达定理能够导出抛物线方程;
得,y2-2pky-2pm=0,再由韦达定理能够导出抛物线方程;(2)由
 =
= ,能够导出△AOB面积的最小值;
,能够导出△AOB面积的最小值;(3)
 =
=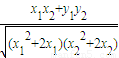 =
=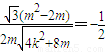 ,由此能求出实数m的取值范围.
,由此能求出实数m的取值范围.解答:解:(1)设直线AB方程为:x=ky+m,抛物线方程为:y2=2px(p>0),
由
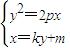 得,y2-2pky-2pm=0,
得,y2-2pky-2pm=0,设A(x1,y1),B(x2,y2),则有
 ,
,由题意,|-2pm|=2m⇒2p=2,
故所求抛物线方程为:y2=2x;
(2)
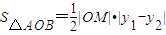
=

 =m
=m .
.(3)
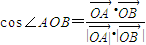 =
=
=
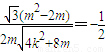 ,
,∴
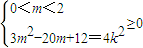 ,
,∴
 .
.点评:本题考查抛物线方程的求法,求△AOB面积的最小值和求实数m的取值范围.解题时要认真审题,仔细挖掘题设中的隐含条件,灵活运用抛物线的性质,合理地进行等价转化.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
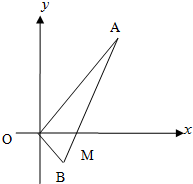 如图,线段AB过x轴正半轴上一点M(m,0)(m>0),端点A、B到x轴距离之积为2m,以x轴为对称轴,过A、O、B三点作抛物线.
如图,线段AB过x轴正半轴上一点M(m,0)(m>0),端点A、B到x轴距离之积为2m,以x轴为对称轴,过A、O、B三点作抛物线.