题目内容
定义域为R的函数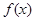 满足
满足 ,当
,当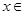 [0,2)时,
[0,2)时,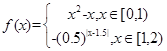 若
若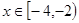 时,
时,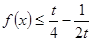 有解,则实数t的取值范围是
有解,则实数t的取值范围是
A.[-2,0) (0,l) (0,l) | B.[-2,0)  [l,+∞) [l,+∞) | C.[-2,l] | D.( ,-2] ,-2]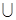 (0,l] (0,l] |
B
解析试题分析: 时,
时, ,
,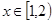 时,
时,
 时,
时, ,由于函数
,由于函数 ,当
,当
当 ,有题知
,有题知 解之当
解之当
考点:函数性质的综合应用.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
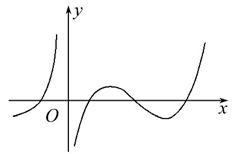
已知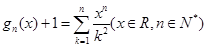 ,则下列说法正确的是( )
,则下列说法正确的是( )
①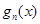 关于点
关于点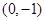 成中心对称
成中心对称
②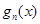 在
在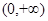 单调递增
单调递增
③当 取遍
取遍 中所有数时不可能存在
中所有数时不可能存在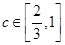 使得
使得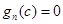
| A.①②③ | B.②③ | C.①③ | D.② |
函数 的值域是( )
的值域是( )
| A.(0,+∞) | B.(0,1) | C.(0,1] | D.[1,+∞) |
 ( )
( )
A. | B. | C. | D. |
函数 的图像( ).
的图像( ).
| A.关于原点对称 | B.关于主线 对称 对称 |
C.关于 轴对称 轴对称 | D.关于直线 对称 对称 |
设函数 ,用二分法求方程
,用二分法求方程 在
在 内近似解的过程中得
内近似解的过程中得 则方程的根落在区间 ( )
则方程的根落在区间 ( )
A. | B. | C. | D.不能确定 |
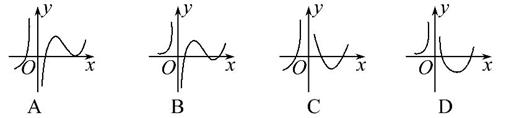
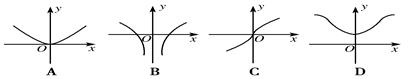
 |≤2,q::x2-2x+1-m2≤0(m>0),若
|≤2,q::x2-2x+1-m2≤0(m>0),若 是
是 的必要而不充分条件,求实数m的取值范围. ks*5*u
的必要而不充分条件,求实数m的取值范围. ks*5*u