题目内容
（本小题满分14分）已知函数
，且
（1）求m的值；
（2）判断
在
上的单调性，并给予证明；
（3）求函数
在区间
上的最值．
【解析】试题解析：（1)由
得：
，即：
，解得：；
（2）函数
在
上为减函数。
证明：设
，则
；
∵ ∴ 
，即
，即
，
∴ 
在上为减函数。
（3）由（1)知：函数
，其定义域为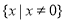
。
∴
，即函数为奇函数。
由（2)知：在
上为减函数，则函数在区间
上为减函数。
∴当
时，取得最大值，最大值为
；
当
时，取得最小值，最小值为
。
考点：本题考查函数的单调性
练习册系列答案
相关题目
，命题若
，则
的否命题是
，则
，则
，则
的前
项和为
,则数列
的前100项和为 （ ）
B．
C．
D．
已知
与y之间的几组数据如下表：
| 1 | 2 | 3 | 4 | 5 | 6 |
y | 0 | 2 | 1 | 3 | 3 | 4 |
假设根据上表数据所得线性回归直线方程为
，若某同学根据上表中的前两组数据（1,0）和（2,2）求得的直线方程为
，则以下结论正确的是（ ）
A.
B.
C.
D.
为定义在
上的奇函数，当
时，
（
为常数)，则
____________.
，函数
在区间
上的最大值是最小值的2倍，则
（ )
D．4
，函数
在区间[
]上的最大值与最小值之差为
，则
D．
，欲使它的前
项的乘积大于
，则
B．
C．
D．