题目内容
函数f(x)=πx-sinx(x∈R)的部分图象是
- A.

- B.

- C.

- D.

D
分析:由f′(x)=π-cosx>0可知f(x)=πx-sinx在R上单调递增,又可判断πx-sinx>x
解答:f′(x)=π-cosx>0恒成立
∴函数f(x)=πx-sinx在R上单调递增,故排除A,B
∵当x=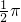 时,
时, 可知πx-sinx>x,故可排除C
可知πx-sinx>x,故可排除C
故选D
点评:本题考查了正弦函数曲线,利用函数图象的变换,以及解析式与函数图象的对应关系,判断出函数图象的大致形状即可.
分析:由f′(x)=π-cosx>0可知f(x)=πx-sinx在R上单调递增,又可判断πx-sinx>x
解答:f′(x)=π-cosx>0恒成立
∴函数f(x)=πx-sinx在R上单调递增,故排除A,B
∵当x=
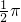 时,
时, 可知πx-sinx>x,故可排除C
可知πx-sinx>x,故可排除C故选D
点评:本题考查了正弦函数曲线,利用函数图象的变换,以及解析式与函数图象的对应关系,判断出函数图象的大致形状即可.

练习册系列答案
相关题目