题目内容
如图3-3-2,在墙壁上挂着一块正方形飞镖板,其边长为16 cm,上面的几个圆圈,分别是半径为2 cm,4 cm,6 cm的同心圆.某人站在3 m之外投掷飞镖,设飞镖投中线上或没有投中飞镖板都不算,可重投,问:
图3-3-2
(1)投中大圆内的概率是多少?
(2)投中小圆与中圆形成的圆环的概率是多少?
(3)投中大圆之外的概率是多少?
思路分析:投中正方形木板上每一点(投中线上或没投中都不算)都是一个基本事件,这一点可以是正方形木板上任意一点,因而基本事件有无限多个,且每个基本事件发生的可能性是相等的,所以投中某一部分的概率只与这部分的几何度量(面积)有关,这符合几何概型的条件.
解:记A={投镖投中大圆内},B={投镖投中小圆与中圆形成的圆环},C={投镖投中大圆之外},S正方形=162=256(cm2),S大圆=π×62=36π(cm2),S中圆=π×42=16π(cm2),S小圆=π×22=4π(cm2).
所以(1)P(A)=![]() ;
;
(2)P(B)=![]() ;
;
(3)P(C)=![]() .
.
所以,(1)投中大圆内的概率是![]() ;
;
(2)投中小圆与中圆形成的圆环的概率是![]() ;
;
(3)投中大圆之外的概率是1-![]() .
.
巧解提示 要准确把握图形的边界与基本事件所表示的区域的关系.如本题,投中线上或投不中都不算,因而投中正方形内各部分的任何一点都是等可能的.

练习册系列答案
相关题目

 +
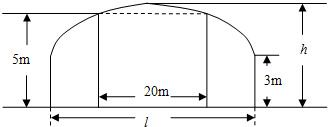
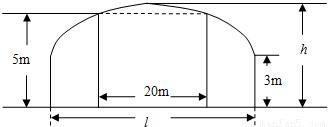
+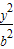 =1的面积公式为S=πab,柱体体积为底面积乘以高.)
=1的面积公式为S=πab,柱体体积为底面积乘以高.)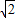 倍,试确定M、N的位置以及h的值,使总造价最少.
倍,试确定M、N的位置以及h的值,使总造价最少.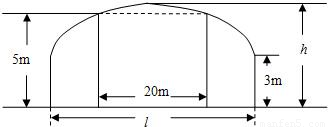
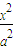 +
+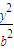 =1的面积公式为S=πab,柱体体积为底面积乘以高.)
=1的面积公式为S=πab,柱体体积为底面积乘以高.)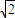 倍,试确定M、N的位置以及h的值,使总造价最少.
倍,试确定M、N的位置以及h的值,使总造价最少.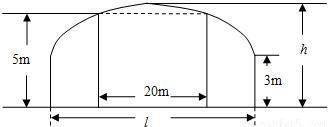
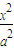 +
+ =1的面积公式为S=πab,柱体体积为底面积乘以高.)
=1的面积公式为S=πab,柱体体积为底面积乘以高.)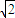 倍,试确定M、N的位置以及h的值,使总造价最少.
倍,试确定M、N的位置以及h的值,使总造价最少.