题目内容
已知函数 ,
,
(I)当 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程;
(II)在区间 内至少存在一个实数
内至少存在一个实数 ,使得
,使得 成立,求实数
成立,求实数 的取值范围.
的取值范围.
【答案】
(I) ;(II)
;(II) .
.
【解析】
试题分析:(I)先把 带入函数解析式,再对函数求导,然后求在已知点的切线的斜率和已知点的坐标,再由点斜式求切线方程;(II)法1:先求函数的导函数,得导函数为0时的根值,讨论根值在区间
带入函数解析式,再对函数求导,然后求在已知点的切线的斜率和已知点的坐标,再由点斜式求切线方程;(II)法1:先求函数的导函数,得导函数为0时的根值,讨论根值在区间 的内外情况,判断原函数在区间
的内外情况,判断原函数在区间 的单调性,从而让原函数在区间
的单调性,从而让原函数在区间 上的最小值小于0,解得
上的最小值小于0,解得 的取值范围.法2:把
的取值范围.法2:把 利用分离变量法分离
利用分离变量法分离 ,构造新的函数,利用导数求新函数在区间
,构造新的函数,利用导数求新函数在区间 上的最小值,让
上的最小值,让 小于最小值就是
小于最小值就是 的取值范围.
的取值范围.
试题解析:(I)当 时,
时, ,
, , 2分
, 2分
曲线 在点
在点 处的切线斜率
处的切线斜率
 ,
,
所以曲线 在点
在点 处的切线方程为
处的切线方程为 . 6分
. 6分
(II)解1:
 7分
7分
当 ,即
,即 时,
时, ,
, 在
在 上为增函数,
上为增函数,
故

 ,所以
,所以
 ,
,
 ,这与
,这与 矛盾 9分
矛盾 9分
当 ,即
,即 时,
时,
若 ,
, ;若
;若 ,
, ,
,
所以 时,
时, 取最小值,因此有
取最小值,因此有
 ,即
,即
 ,
,
解得 ,这与
,这与 矛盾;
12分
矛盾;
12分
当 即
即 时,
时, ,
, 在
在 上为减函数,所以
上为减函数,所以

 ,所以
,所以 ,解得
,解得 ,这符合
,这符合 .
.
综上所述, 的取值范围为
的取值范围为 .
15分
.
15分
解2:有已知得: ,
8分
,
8分
设 ,
,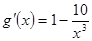 ,
10分
,
10分
 ,
, ,所以
,所以 在
在 上是减函数. 12分
上是减函数. 12分
 ,故
,故 的取值范围为
的取值范围为 15分
15分
考点:1、利用导函数求切线方程;2、导函数的性质;3、分离变量法.

练习册系列答案
相关题目
 .
. .
. ,
, .
.